
【题目】四面体 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,则此四面体外接球的表面积为
,则此四面体外接球的表面积为 ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
分析:由△BCD中,CB=DB=2,∠CBD=60°,可知△BCD是等边三角形,∠ABC=∠ABD=60°,可得AD=AC=![]() ,求出底面△BCD的外接圆半径r=
,求出底面△BCD的外接圆半径r=![]() .利用球心到圆心构造直角三角形即可求解外接球R.
.利用球心到圆心构造直角三角形即可求解外接球R.
详解:
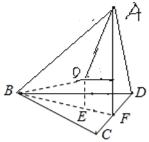
由题意,△BCD中,CB=DB=2,∠CBD=60°,
可知△BCD是等边三角形,BF=![]()
∴△BCD的外接圆半径r=![]() =BE,FE=
=BE,FE=![]()
∵∠ABC=∠ABD=60°,可得AD=AC=![]() ,
,
可得AF=![]()
∴AF⊥FB
∴AF⊥BCD,
∴四面体A﹣BCD高为AF=![]() .
.
设:外接球R,O为球心,OE=m
可得:r2+m2=R2……①,
(![]() )2+EF2=R2……②
)2+EF2=R2……②
由①②解得:R=![]() .
.
四面体外接球的表面积:S=4πR2=![]() .
.
故选:A.


科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下顶点、右顶点、右焦点分别为B2、B1、A、F,延长B1F与AB2交于点P,若∠B1PA为钝角,则此椭圆的离心率e的取值范围为_____.
的上、下顶点、右顶点、右焦点分别为B2、B1、A、F,延长B1F与AB2交于点P,若∠B1PA为钝角,则此椭圆的离心率e的取值范围为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人各有![]() 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有![]() 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有![]() 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出![]() 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间![]() ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 为正方形,四边形
为正方形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若过直线![]() 的一个平面与线段
的一个平面与线段![]() 和
和![]() 分别相交于点
分别相交于点![]() 和
和![]() (点
(点![]() 与点
与点![]() 均不重合),求证:
均不重合),求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理” 的原则,规定参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有![]() 三家社区医院,并且他们的选择是等可能的、相互独立的.
三家社区医院,并且他们的选择是等可能的、相互独立的.
(1)求甲、乙两人都选择![]() 社区医院的概率;
社区医院的概率;
(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设在4名参加保险人员中选择![]() 社区医院的人数为
社区医院的人数为![]() ,求
,求![]() 的分布列和数学期望及方差.
的分布列和数学期望及方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com