
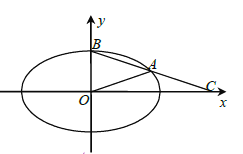
【题目】如图所示,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上位于第一象限上的点,
上位于第一象限上的点,![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() 的面积为6.
的面积为6.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,设椭圆
有且只有一个公共点,设椭圆![]() 的两焦点到直线
的两焦点到直线![]() 的距离分别是
的距离分别是![]() ,
,![]() ,试问
,试问![]() 是否为定值?若是,求出其值;若不是,说明理由.
是否为定值?若是,求出其值;若不是,说明理由.
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小相同的5个小球,编号分别为0,1,2,3,4,现从中随机地摸一个球,记下编号后放回,连摸3次,若摸出的3个小球的最大编号与最小编号之差为2,则共有________种不同的摸球方法(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三位数中,如果百位数字、十位数字、个位数字刚好能构成等差数列,则称为“等差三位数”,例如:147,642,777,420等等.等差三位数的总个数为( )
A.32B.36C.40D.45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:![]() 和圆C2:(x-6)2+(y-1)2=1,过圆C2上一点P作圆的切线MN交抛物线C,于M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
和圆C2:(x-6)2+(y-1)2=1,过圆C2上一点P作圆的切线MN交抛物线C,于M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
A.4x-3y-22=0B.4x-3y-16=0C.2x-y-11+5=0D.4x-3y-26=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,动点
,动点![]() ,线段QF与圆F相交于点P,线段PQ的长度与点Q到y轴的距离相等.
,线段QF与圆F相交于点P,线段PQ的长度与点Q到y轴的距离相等.
(Ⅰ)求动点Q的轨迹W的方程;
(Ⅱ)过点![]() 作两条互相垂直的直线与W的交点分别是M和N(M在N的上方,A,M,N为不同的三点),求向量
作两条互相垂直的直线与W的交点分别是M和N(M在N的上方,A,M,N为不同的三点),求向量![]() 在y轴正方向上的投影的取值范围.
在y轴正方向上的投影的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com