
【题目】设![]() ,函数
,函数![]() .
.
(Ⅰ)讨论函数![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)已知![]() (
(![]() 是自然对数的底数)和
是自然对数的底数)和![]() 是函数
是函数![]() 的两个不同的零点,求
的两个不同的零点,求![]() 的值并证明:
的值并证明:![]() .
.
【答案】(Ⅰ)①当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,无极值,②当
,无极值,②当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,递减区间是
,递减区间是![]() ,函数
,函数![]() 的极大值为
的极大值为![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
试题(Ⅰ)分别令![]() 及
及![]() 分情况讨论;(Ⅱ)由已知得
分情况讨论;(Ⅱ)由已知得![]() ,由(Ⅰ)函数
,由(Ⅰ)函数![]() 在
在![]() 递减及
递减及![]() ,
,![]() ,可知函数
,可知函数![]() 在区间
在区间![]() 有唯一零点,由此得证.
有唯一零点,由此得证.
试题解析:(Ⅰ)由已知得![]()
![]() ,
,![]() ,
,
①若![]() ,则
,则![]() ,
,![]() 是区间
是区间![]() 上的增函数,无极值;
上的增函数,无极值;
②若![]() ,令
,令![]() ,得
,得![]() ,
,
在区间![]() 上,
上,![]() ,函数
,函数![]() 是增函数,
是增函数,
在区间![]() 上,
上,![]() ,函数
,函数![]() 是减函数,
是减函数,
所以在区间![]() 上,
上,![]() 的极大值为
的极大值为![]() .
.
综上所述,①当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,无极值;②当
,无极值;②当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,递减区间是
,递减区间是![]() ,函数
,函数![]() 的极大值为
的极大值为![]() .
.
(Ⅱ)因为![]() ,所以
,所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,
由(Ⅰ)函数![]() 在
在![]() 递减,故函数
递减,故函数![]() 在区间
在区间![]() 有唯一零点,因此
有唯一零点,因此![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】一种新的验血技术可以提高血液检测效率.现某专业检测机构提取了![]() 份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中
份血液样本,其中只有1份呈阳性,并设计了如下混合检测方案:先随机对其中![]() 份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这
份血液样本分别取样,然后再混合在一起进行检测,若检测结果为阴性,则对另外3份血液逐一检测,直到确定呈阳性的血液为止;若检测结果呈阳性,测对这![]() 份血液再逐一检测,直到确定呈阳性的血液为止.
份血液再逐一检测,直到确定呈阳性的血液为止.
(1)若![]() ,求恰好经过3次检测而确定呈阳性的血液的事件概率;
,求恰好经过3次检测而确定呈阳性的血液的事件概率;
(2)若![]() ,宜采用以上方案检测而确定呈阳性的血液所需次数为
,宜采用以上方案检测而确定呈阳性的血液所需次数为![]() ,
,
①求![]() 的概率分布;
的概率分布;
②求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个同样的红球、两个同样的黑球和两个同样的白球放入下列6个格中,要求同种颜色的球不相邻,则可能的放球方法共有______种.(用数字作答)
1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位在2019年重阳节组织50名退休职工(男、女各25名)旅游,退休职工可以选择到甲、乙两个景点其中一个去旅游.他们最终选择的景点的结果如下表:
男性 | 女性 | |
甲景点 | 20 | 10 |
乙景点 | 5 | 15 |
(1)据此资料分析,是否有![]() 的把握认为选择哪个景点与性别有关?
的把握认为选择哪个景点与性别有关?
(2)按照游览不同景点用分层抽样的方法,在女职工中选取5人,再从这5人中随机抽取2人进行采访,求这2人游览的景点不同的概率.
附: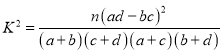 ,
,![]() .
.
P( | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,圆
为坐标原点,圆![]() :
:![]() ,定点
,定点![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 的半径
的半径![]() 于点
于点![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)不垂直于![]() 轴且不过
轴且不过![]() 点的直线
点的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]() 、
、![]() 的斜率之和为0,则动直线
的斜率之和为0,则动直线![]() 是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由.
是否一定经过一定点?若过一定点,则求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知多面体ABCDEF中,四边形ABFE为正方形,![]() ,
,![]() ,G为AB的中点,
,G为AB的中点,![]() .
.
(1)求证:![]() 平面CDEF;
平面CDEF;
(2)求平面ACD与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
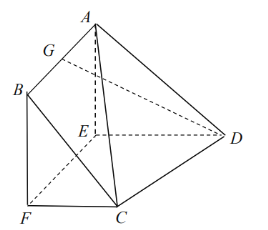
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.
(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com