
【题目】已知f(x)是定义在(0,+∞)上的单调递减函数,f′(x)是其导函数,若 ![]() >x,则下列不等关系成立的是( )
>x,则下列不等关系成立的是( )
A.f(2)<2f(1)
B.3f(2)>2f(3)
C.ef(e)<f(e2)
D.ef(e2)>f(e3)
【答案】C
【解析】解:令g(x)= ![]() ,故g′(x)=
,故g′(x)= ![]() ,
,
∵f(x)是定义在(0,+∞)上的单调递减函数,f′(x)是其导函数,
∴f′(x)<0,
∵ ![]() >x,
>x,
∴xf′(x)﹣f(x)>0,
∴函数g(x)在(0,+∞)上是增函数,
故 ![]() >
> ![]() >
> ![]() ,
, ![]() >
> ![]() >
> ![]() ,
,
故2f(3)>3f(2),f(2)>2f(1),
f(e3)>ef(e2),ef(e)<f(e2);
所以答案是:C.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左,右焦点分别为F1 , F2 , 过F1任作一条与两坐标轴都不垂直的直线,与C交于A,B两点,且△ABF2的周长为8.当直线AB的斜率为
的左,右焦点分别为F1 , F2 , 过F1任作一条与两坐标轴都不垂直的直线,与C交于A,B两点,且△ABF2的周长为8.当直线AB的斜率为 ![]() 时,AF2与x轴垂直. (I)求椭圆C的方程;
时,AF2与x轴垂直. (I)求椭圆C的方程;
(Ⅱ)在x轴上是否存在定点M,总能使MF1平分∠AMB?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班开展一次智力竞赛活动,共a,b,c三个问题,其中题a满分是20分,题b,c满分都是25分.每道题或者得满分,或者得0分.活动结果显示,全班同学每人至少答对一道题,有1名同学答对全部三道题,有15名同学答对其中两道题.答对题a与题b的人数之和为29,答对题a与题c的人数之和为25,答对题b与题c的人数之和为20.则该班同学中只答对一道题的人数是;该班的平均成绩是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”). 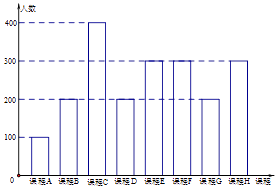
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组M”中选择F课程或G课程的同学,并且这些同学以自愿报名缴费的方式参加活动.选择F课程的学生中有x人参加科学营活动,每人需缴纳2000元,选择G课程的学生中有y人参加该活动,每人需缴纳1000元.记选择F课程和G课程的学生自愿报名人数的情况为(x,y),参加活动的学生缴纳费用总和为S元.
(ⅰ)当S=4000时,写出(x,y)的所有可能取值;
(ⅱ)若选择G课程的同学都参加科学营活动,求S>4500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
(Ⅰ)求获得参赛资格的人数;
(Ⅱ)若大赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ![]() ,求甲在初赛中答题个数X的分布列及数学期望E(X)
,求甲在初赛中答题个数X的分布列及数学期望E(X)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为实常数,函数f(x)=ex﹣ax﹣1(e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a≤1,函数f(x)有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ,g(x)=ax+b.
,g(x)=ax+b.
(1)若函数h(x)=f(x)﹣g(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)若直线g(x)=ax+b是函数f(x)=lnx﹣ ![]() 图象的切线,求a+b的最小值;
图象的切线,求a+b的最小值;
(3)当b=0时,若f(x)与g(x)的图象有两个交点A(x1 , y1),B(x2 , y2),求证:x1x2>2e2 .
(取e为2.8,取ln2为0.7,取 ![]() 为1.4)
为1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C. 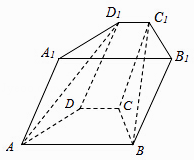
(1)求证:AD1⊥BC;
(2)若直线DD1与直线AB所成角为 ![]() ,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com