
| A. | 50 | B. | 80 | C. | 90 | D. | 100 |
分析 由题意得这个小球在这次运动中所经过的总路程Sn=2×10+2×10×$\frac{4}{5}$+2×10×($\frac{4}{5}$)2+2×10×($\frac{4}{5}$)3+…+2×10×($\frac{4}{5}$)n-10,由此利用极限思想能求出结果.
解答 解:∵一个弹性小球从10米自由落下,着地后反弹到原来高度的$\frac{4}{5}$处,再自由落下,又弹回到上一次高度的$\frac{4}{5}$处,
∴这个小球在这次运动中所经过的总路程为:
Sn=2×10+2×10×$\frac{4}{5}$+2×10×($\frac{4}{5}$)2+2×10×($\frac{4}{5}$)3+…+2×10×($\frac{4}{5}$)n-10
=2×$\frac{10[1-(\frac{4}{5})^{n}]}{1-\frac{4}{5}}$-10,
假设这个小球能无限次反弹,
则这个小球在这次运动中所经过的总路程:
S=$\underset{lim}{n→∞}{S}_{n}$=$\underset{lim}{n→∞}${2×$\frac{10[1-(\frac{4}{5})^{n}]}{1-\frac{4}{5}}$-10}=2×$\frac{10}{1-\frac{4}{5}}$-10=90.
故选:C.
点评 本题考查小球在运动中经过路程的求法,是中档题,解题时要认真审题,注意等比数列的性质和极限思想的合理运用.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
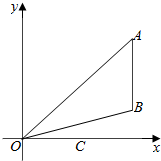 已知O为坐标原点,向量$\overrightarrow{OA}$=(3cosx,3sinx),$\overrightarrow{OB}$=(3cosx,sinx),$\overrightarrow{OC}$=($\sqrt{3}$,0),x∈(0,$\frac{π}{2}$).
已知O为坐标原点,向量$\overrightarrow{OA}$=(3cosx,3sinx),$\overrightarrow{OB}$=(3cosx,sinx),$\overrightarrow{OC}$=($\sqrt{3}$,0),x∈(0,$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,1) | B. | (0,$\frac{2}{3}$)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com