Question

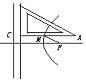
如图所示，把一根直尺固定在图上直线l的位置，把一块三角尺的一条直角边紧靠着直尺的边缘，再把一条细绳的一端固定在三角尺的另一条直角边的一点A，取绳长等于点A到直角顶点C的长（即点A到直线l的距离），并且把绳子的另一端固定在图板上的一点F，用铅笔尖扣着绳子，使点A到笔尖的一段绳子紧靠着三角尺，然后将三角尺沿着直尺上下滑动，笔尖就在图板上描出了一条曲线。说出这条曲线有什么特征？

Answer 1

答案：
解析：

解法一：以l为y轴，过点F垂直于l的直线为x轴建立直角坐标系（如图所示），则定点F（p,0） 设动点M（x,y），由抛物线定义得： 化简得： y2=2px－p2(p＞0) 解法二：以定点F为原点，过点F垂直于l的直线为x轴建立直角坐标系（如右图所示）， 则定点F（0，0），l的方程为x=－p。 设动点M（x,y)，由抛物线定义得： =|x+p| 化简得： y2=2px+p2(p＞0) 解法三：取过焦点F且垂直于准线l的直线为x轴，x轴与l交于K，以线段KF的垂直平分线为y轴建立直角坐标系，如右图所示，则有F（,0）,l的方程为x=－。 设动点M（x,y），由抛物线定义得： 化简得 y2=2px(p＞0)