
【题目】如下图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b. (0 <φ < π)
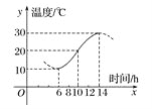
(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式.
【答案】(1)这段时间的最大温差是30(℃);(2)y=10sin![]() +20,x∈[6,14].
+20,x∈[6,14].
【解析】试题分析:(1)由图象的最高点与最低点易于求出这段时间的最大温差;
(2)A、b可由图象直接得出,ω由周期求得,然后通过特殊点求φ,则问题解决.
试题解析:
(1)由图知,这段时间的最大温差是30(℃).
(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象.
∴![]() ·
·![]() =14-6,解得ω=
=14-6,解得ω=![]() .
.
由图知,A=![]() (30-10)=10,b=
(30-10)=10,b=![]() (30+10)=20,这时y=10sin
(30+10)=20,这时y=10sin![]() +20,
+20,
将x=6,y=10代入上式可取φ=![]() π.
π.
综上所求的解析式为y=10sin![]() +20,x∈[6,14].
+20,x∈[6,14].


科目:高中数学 来源: 题型:
【题目】某城市在发展过程中,交通状况逐渐受到有关部门的关注,据有关统计数据显示,从上午6点到中午12点,车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出: y= 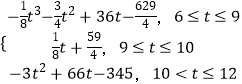
求从上午6点到中午12点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+1|+|2x﹣a|.
(1)若f(x)的最小值为2,求a的值;
(2)若f(x)≤|2x﹣4|的解集包含[﹣2,﹣1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的定义域为
的定义域为![]() ,且存在非零常数
,且存在非零常数![]() ,对任意
,对任意![]() ,
, ![]() 恒成立,则称
恒成立,则称![]() 为线周期函数,
为线周期函数, ![]() 为
为![]() 的线周期.
的线周期.
(Ⅰ)下列函数①![]() ,②
,②![]() ,③
,③![]() (其中
(其中![]() 表示不超过
表示不超过![]() 的最大整数),是线周期函数的是(直接填写序号);
的最大整数),是线周期函数的是(直接填写序号);
(Ⅱ)若![]() 为线周期函数,其线周期为
为线周期函数,其线周期为![]() ,求证:函数
,求证:函数![]() 为周期函数;
为周期函数;
(Ⅲ)若![]() 为线周期函数,求
为线周期函数,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接党的“十九大”胜利召开与响应国家交给的“提速降费”任务,某市移动公司欲提供新的资费套餐(资费包含手机月租费、手机拨打电话费与家庭宽带上网费)。其中一组套餐变更如下:
原方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
18元/月 | 0.2元/分钟 | 50元/月 |
新方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
58元/月 | 前100分钟免费, 超过部分 | 免费 |
(1)客户甲(只有一个手机号和一个家庭宽带上网号)欲从原方案改成新方案,设其每月手机通话时间为![]() 分钟(
分钟(![]() ),费用
),费用![]() 原方案每月资费-新方案每月资费,写出
原方案每月资费-新方案每月资费,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)经过统计,移动公司发现,选这组套餐的客户平均月通话时间![]() 分钟,为能起到降费作用,求
分钟,为能起到降费作用,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C的两个焦点是F1、F2 , 过F1的直线与椭圆C交于P、Q,若|PF2|=|F1F2|,且5|PF1|=6|F1Q|,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com