
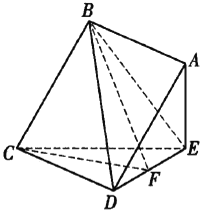
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 平面
平面![]() .已知
.已知![]() ,
,![]() 为线段
为线段![]() 上的一点,二面角
上的一点,二面角![]() 与二面角
与二面角![]() 的大小相等.则
的大小相等.则![]() 的长为______.
的长为______.
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .若四边形
.若四边形![]() 为矩形,线段
为矩形,线段![]() 与
与![]() 交于点
交于点![]() .
.

(1)证明:![]() ∥平面
∥平面![]() .
.
(2)求二面角![]() 的大小。
的大小。
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.

(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 当
当![]() 时,判断直线
时,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
![]() 若直线
若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试中500名学生的物理(满分为150分)成绩服从正态分布![]() ,数学成绩的频率分布直方图如图所示.
,数学成绩的频率分布直方图如图所示.

(Ⅰ)如果成绩大于135分为特别优秀,那么本次考试中的物理、数学特别优秀的大约各有多少人?
(Ⅱ)如果物理和数学两科都特别优秀的共有4人,是否有99.9%的把握认为物理特别优秀的学生,数学也特别优秀?
附:①若![]() ,则
,则![]()
②表及公式:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com