
【题目】如图长方体![]() 中,
中,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点
的中点

(1)求证:平面![]() 平面
平面![]() ;
;
(2)请在答题卡图形中画出直线![]() 与平面
与平面![]() 的交点
的交点![]() (保留必要的辅助线),写出画法并计算
(保留必要的辅助线),写出画法并计算![]() 的值(不必写出计算过程).
的值(不必写出计算过程).
【答案】(1)见证明;(2) ![]() ;画图见解析
;画图见解析
【解析】
(1)推导出![]() 平面
平面![]() ,得出
,得出![]() ,得出
,得出![]() ,从而得到
,从而得到![]() ,进而证出
,进而证出![]() 平面
平面![]() ,由此证得平面
,由此证得平面![]() 平面
平面![]() .
.
(2)根据通过辅助线推出线面平行再推出线线平行,再根据“一条和平面不平行的直线与平面的公共点即为直线与平面的交点”得到![]() 点位置,然后计算
点位置,然后计算![]() 的值.
的值.
(1)证明:在长方体![]() 中,
中,![]() ,
,
![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,所以
的中点,所以![]() 平面
平面![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,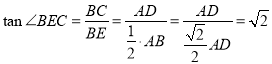 ,
,
所以![]() ,因为在
,因为在![]() 中,
中,![]() ,所以
,所以![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(2)
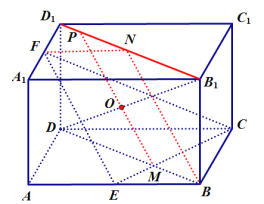
如图所示:设![]() ,连接
,连接![]() ,取
,取![]() 中点记为
中点记为![]() ,过
,过![]() 作
作![]() ,且
,且![]() ,则
,则![]() .
.
证明:因为![]() 为
为![]() 中点,所以
中点,所以![]() 且
且![]() ;又因为
;又因为![]() ,且
,且![]() ,所以
,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 为平行四边形,则
为平行四边形,则![]() ;又因为
;又因为![]() ,所以
,所以![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;又因为
;又因为![]() ,则
,则![]() ,
,![]() 平面
平面![]() ,即点
,即点![]() 为直线
为直线![]() 与平面
与平面![]() 的交点;
的交点;
因为![]() ,所以
,所以![]() ,则
,则![]() ;且有上述证明可知:四边形
;且有上述证明可知:四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】办公室装修一新,放些植物花草可以清除异味,公司提供绿萝、文竹、碧玉、芦荟4种植物供员工选择,每个员工任意选择2种,则员工甲和乙选择的植物全不同的概率为:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( ) 
A.![]() 海里
海里
B.![]() 海里
海里
C.![]() 海里
海里
D.40海里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“若A则B”为真命题,而“若B则C”的逆否命题为真命题,且“若A则B”是“若C则D”的充分条件,而“若D则E”是“若B则C”的充要条件,则¬B是¬E的____条件;A是E的____条件.(填“充分”“必要”、“充要”或“既不充分也不必要”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂要制造A种电子装置45台,B种电子装置55台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳分别为6个和6个,求两种薄钢板各用多少张,才能使总的面积最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有同一型号的汽车100辆,为了解这种汽车每耗油![]() 所行路程的情况,现从中随机地抽出10辆,在同一条件下进行耗油
所行路程的情况,现从中随机地抽出10辆,在同一条件下进行耗油![]() 所行路程的试验,得到如下样本数据(单位:km):13.7, 12.7, 14.4, 13.8, 13.3 ,12.5 ,13.5 ,13.6 ,13.1 ,13.4,
所行路程的试验,得到如下样本数据(单位:km):13.7, 12.7, 14.4, 13.8, 13.3 ,12.5 ,13.5 ,13.6 ,13.1 ,13.4,
并分组如下:
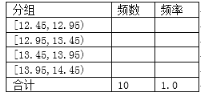
(1)完成上面的频率分布表;
(2)根据上表,在坐标系中画出频率分布直方图.
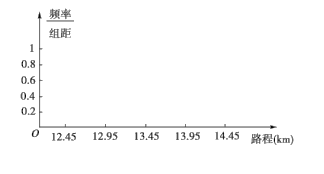
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com