
【题目】某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别做记录,抽查数据如下:
甲车间:102,101,99,98,103,98,99;
乙车间:110,115,90,85,75,115,110.
(1)问:这种抽样是何种抽样方法;
(2)估计甲、乙两车间包装产品的质量的均值与方差,并说明哪个均值的代表性好,哪个车间包装产品的质量较稳定.
【答案】
(1)
解:由于是每隔1小时抽取一包产品,是等间隔抽取,属于系统抽样
(2)
解:甲的平均数为:![]() (102+101+99+98+103+98+99)=100
(102+101+99+98+103+98+99)=100
乙的平均数为:![]() (110+115+90+85+75+115+110)=100
(110+115+90+85+75+115+110)=100
∴两人的均值相同,
甲的方差为: ![]() [(102﹣100)2+(101﹣100)2+(99﹣100)2+(103﹣100)2+(98﹣100)2+(99﹣100)2+(98﹣100)2]=
[(102﹣100)2+(101﹣100)2+(99﹣100)2+(103﹣100)2+(98﹣100)2+(99﹣100)2+(98﹣100)2]=![]() .
.
乙的方差为: ![]() [(110﹣100)2+(115﹣100)2+(90﹣100)2+(85﹣100)2+(75﹣100)2+(115﹣100)2+(110﹣100)2]=
[(110﹣100)2+(115﹣100)2+(90﹣100)2+(85﹣100)2+(75﹣100)2+(115﹣100)2+(110﹣100)2]=![]() .
.
∴s2甲<s2乙,
∴甲车间包装的产品质量较稳定
【解析】(1)每隔1小时抽取一包产品,等间隔抽取,属于系统抽样.(2)做出两组数据的平均数和方差,把两组数据的方差和平均数进行比较,看出平均数相等,而甲的方差小于乙的方差,得到甲车间比较稳定.
【考点精析】利用系统抽样方法对题目进行判断即可得到答案,需要熟知把总体的单位进行排序,再计算出抽样距离,然后按照这一固定的抽样距离抽取样本;第一个样本采用简单随机抽样的办法抽取.


科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
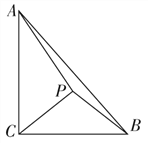
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点
的焦点![]() 与椭圆
与椭圆![]() :
: ![]() 的一个焦点重合,点
的一个焦点重合,点![]() 在抛物线上,过焦点
在抛物线上,过焦点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点.
两点.
(Ⅰ)求抛物线![]() 的方程以及
的方程以及![]() 的值;
的值;
(Ⅱ)记抛物线的准线![]() 与
与![]() 轴交于点
轴交于点![]() ,试问是否存在常数
,试问是否存在常数![]() ,使得
,使得![]() 且
且![]() 都成立?若存在,求出实数
都成立?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
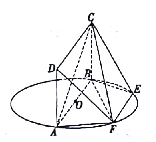
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在圆
在圆![]() 上,且
上,且![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面垂直,且
所在的平面垂直,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在了点
上是否存在了点![]() ,使得
,使得![]() 平面
平面![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(Ⅱ)若函数![]() 在其定义域上是增函数,求实数
在其定义域上是增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,函数
时,函数![]() 的两个极值点为
的两个极值点为![]() ,且
,且![]() ,若不等式
,若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且sinA+![]() cosA=2.
cosA=2.
(Ⅰ)求角A的大小;
(Ⅱ)现给出三个条件:①a=2;②B=45°;③c= ![]() .试从中选出两个可以确△ABC的条件,写出你的选择,并以此为依据求△ABC的面积.(只写出一个方案即可)
.试从中选出两个可以确△ABC的条件,写出你的选择,并以此为依据求△ABC的面积.(只写出一个方案即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC是边长为1的正三角形,点P1 , P2 , P3四等分线段BC(如图所示).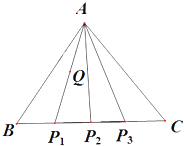
(1)求 ![]()
![]() +
+ ![]()
![]() 的值;
的值;
(2)Q为线段AP1上一点,若 ![]() =m
=m ![]() +
+ ![]()
![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com