练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

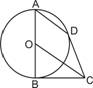
    如右图所示，AB为⊙O的直径，BC、CD为⊙O的切线，B、D为切点.

    （Ⅰ）求证；AD∥OC；

    （Ⅱ）若⊙O的半径为1，求AD·OC的值.

                                                          

     

    【答案】

     

    （Ⅰ）AD∥OC

    （Ⅱ）AD·OC=2

    【解析】（1） 解：（Ⅰ）证明：如图，连接DB、OD,

          BC、CD是⊙O的两条切线

    BD⊥OC,                   ……2分

       又AB为⊙O的直径，AD⊥DB，，

                                                    ……6分

    （Ⅱ）               ……8分

                             ……12分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

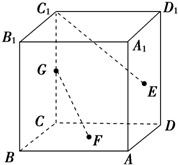    精英家教网如右图所示，正方体ABCD-A1B1C1D1中，E、F分别是正方形ADD1A1和ABCD的中心，G是CC1的中点，设GF、C1E与AB所成的角分别为α、β，则α+β等于（　　）
    A、120°B、60°C、75°D、90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

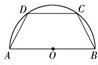    精英家教网如右图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•孝感模拟）在两道题中选择其中一道题作答，若两道都选，按前一道作答结果计分．
    （1）（几何证明选讲题）如右图所示AC和AB分别是圆O的切线，且OC=3，AB=4，延长AO到D点，则△ABD的面积是
    48
    5
    48
    5

    （2）（坐标系与参数方程题）已知圆的极坐标方程为ρ=2COSθ，则该圆的圆心到直线ρsinθ+2ρcosθ=1的距离是
    		5
    5
    		5
    5
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010年本溪市普通高中高二下学期期末考试（理科）数学卷 题型：解答题

    如右图所示，AB为⊙O的直径，BC、CD为⊙O的切线，B、D为切点.
    （Ⅰ）求证；AD∥OC；
    （Ⅱ）若⊙O的半径为1，求AD·OC的值.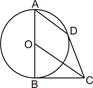

    查看答案和解析>>

    同步练习册答案