
【题目】已知函数 ![]() 为偶函数,且函数的y=f(x)图象相邻的两条对称轴间的距离为
为偶函数,且函数的y=f(x)图象相邻的两条对称轴间的距离为 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)将y=f(x)的图象向右平移 ![]() 个单位后,再将所得的图象上个点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在
个单位后,再将所得的图象上个点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在 ![]() 上的最值.
上的最值.
【答案】
(1)解:函数f(x)= ![]() sin(ωx+φ)﹣cos(ωx+φ)=2sin(ωx+φ﹣
sin(ωx+φ)﹣cos(ωx+φ)=2sin(ωx+φ﹣ ![]() ),…1分
),…1分
因为函数是偶函数,
所以φ﹣ ![]() =kπ+
=kπ+ ![]() ,k∈Z,解得:φ=kπ+
,k∈Z,解得:φ=kπ+ ![]() ,k∈Z,
,k∈Z,
∵﹣ ![]() <φ<0,
<φ<0,
∴φ=﹣ ![]() .
.
函数y=f(x)图象的两相邻对称轴间的距离为 ![]() ,
,
所以T=π,T= ![]() =π,所以ω=2;
=π,所以ω=2;
f(x)=2sin(2x﹣ ![]() )=﹣2cos2x,…5分
)=﹣2cos2x,…5分
则f( ![]() )=﹣2cos(2×
)=﹣2cos(2× ![]() )=﹣2cos(
)=﹣2cos( ![]() ﹣
﹣ ![]() )=﹣
)=﹣ ![]()
(2)解:由函数图象的变换可知,y=g(x)=﹣2cos( ![]() x﹣
x﹣ ![]() ),
),
由2kπ≤ ![]() x﹣
x﹣ ![]() ≤2kπ+π,k∈Z,解得:4kπ+
≤2kπ+π,k∈Z,解得:4kπ+ ![]() ≤x≤4kπ+
≤x≤4kπ+ ![]() ,k∈Z,
,k∈Z,
即函数y=g(x)的单调递增区间为:[4kπ+ ![]() ,4kπ+
,4kπ+ ![]() ]k∈Z,
]k∈Z,
由2kπ+π≤ ![]() x﹣
x﹣ ![]() ≤2kπ+2π,k∈Z,解得:4kπ+
≤2kπ+2π,k∈Z,解得:4kπ+ ![]() ≤x≤4kπ+
≤x≤4kπ+ ![]() ,k∈Z,
,k∈Z,
即函数y=g(x)的单调递减区间为:[4kπ+ ![]() ,4kπ+
,4kπ+ ![]() ]k∈Z,
]k∈Z,
∵x∈ ![]() ,
,
∴结合函数的单调性可知:
当 ![]() x﹣
x﹣ ![]() =0,即x=
=0,即x= ![]() 时,y=g(x)最小值为﹣2
时,y=g(x)最小值为﹣2
当 ![]() x﹣
x﹣ ![]() =﹣
=﹣ ![]() ,即x=﹣
,即x=﹣ ![]() 时,y=g(x)最大值为0
时,y=g(x)最大值为0
【解析】(1)通过两角差的正弦函数化简函数的表达式,求出函数的周期,利用函数是偶函数求出φ,然后求解 ![]() 的值.(2)由函数图象的变换可求g(x)=﹣2cos(
的值.(2)由函数图象的变换可求g(x)=﹣2cos( ![]() x﹣
x﹣ ![]() ),利用余弦函数的单调性可求y=g(x)的单调区间,由x∈
),利用余弦函数的单调性可求y=g(x)的单调区间,由x∈ ![]() ,结合函数的单调性可求最大值.
,结合函数的单调性可求最大值.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|< ![]() ,ω>0)的图象如图所示,函数f(x)=g(x)+
,ω>0)的图象如图所示,函数f(x)=g(x)+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x
sin2x 
(1)如果 ![]() ,且g(x1)=g(x2),求g(x1+x2)的值;
,且g(x1)=g(x2),求g(x1+x2)的值;
(2)当﹣ ![]() ≤x≤
≤x≤ ![]() 时,求函数f(x)的最大值、最小值及相应的x值;
时,求函数f(x)的最大值、最小值及相应的x值;
(3)已知方程f(x)﹣k=0在 ![]() 上只有一解,则k的取值集合.
上只有一解,则k的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点.求证:平面EFG⊥平面EMN.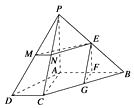
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且 ![]() bcosA=asinB.
bcosA=asinB.
(1)求角A的大小;
(2)若a=6,△ABC的面积是9 ![]() ,求三角形边b,c的长.
,求三角形边b,c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+2x+c的对称轴为x=1,g(x)=x+ ![]() (x>0).
(x>0).
(1)求函数g(x)的最小值及取得最小值时x的值;
(2)试确定c的取值范围,使g(x)﹣f(x)=0至少有一个实根;
(3)若F(x)=﹣f(x)+4x+c,存在实数t,对任意x∈[1,m],使F(x+t)≤3x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC. 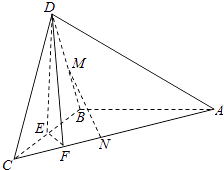
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角B﹣PE﹣D的余弦值.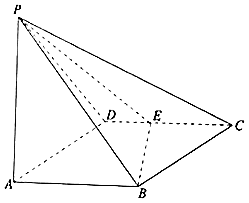
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com