【题目】已知函数f(x)的图像与函数h(x)=
的图像关于点Ａ（0，1）对称。
（１）求函数f(x)的解析式；
（２）若g(x)＝xf(x)＋ax，且g(x)在区间（0,4］上为减函数，求实数a的取值范围。
【答案】（1）
；（2）(－∞，－10].
【解析】试题分析：（1）利用函数关于点A（0，1）对称，求出函数的解析式．
（2）利用二次函数的图象和性质得到对称轴与区间的关系．
试题解析：
(1)∵f(x)的图象与h(x)的图象关于点A(0,1)对称，设f(x)图象上任意一点坐标为B(x，y)，其关于A(0,1)的对称点B′(x′，y′)，
则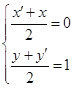
∴ 
∵B′(x′，y′)在h(x)上，∴y′＝x′＋
.
∴2－y＝－x－
，∴y＝x＋ +2，
即f(x) ＝x＋ +2.
(2)∵g(x)＝xf(x)+ax=x2+(a+2)x+1且g(x)在(0,4]上为减函数，
∴
≥4，
即a≤－10.
∴a的取值范围为(－∞，－10]．
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案科目：高中数学 来源： 题型：
【题目】近年来，空气质量成为人们越来越关注的话题，空气质量指数（
，简称
）是定量描述空气质量状况的指数，空气质量按照
大小分为六级， 
为优； 
为良； 
为轻度污染； 
为中度污染； 
为重度污染；大于300为严重污染．环保部门记录了2017年某月哈尔滨市10天的
的茎叶图如下：
（1）利用该样本估计该地本月空气质量优良（
）的天数；（按这个月总共30天计算）
（2）现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究，求抽取的2天中至少有一天空气质量是优的概率；
（3）将频率视为概率，从本月中随机抽取3天，记空气质量优良的天数为
，求
的概率分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
同时满足：①对于定义域上的任意
，恒有
；②对于定义域上的任意
， 
，当
时，恒有
，则称函数
为“理想函数”.在下列三个函数中：（1）
；（2）
；（3）
.“理想函数”有__________．（只填序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为
上的偶函数，当
时， 
.对于结论
（1）当
时， 
；（2）函数
的零点个数可以为4,5,7；
（3）若
，关于
的方程
有5个不同的实根，则
；
（4）若函数
在区间
上恒为正，则实数
的范围是
.
说法正确的序号是__________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中，设BC的中点为M，GH的中点为N.
(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由).
(2)判断平面BEG与平面ACH的位置关系，并证明你的结论.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，l是过定点P(4,2)且倾斜角为α的直线；在极坐标系(以坐标原点O为极点，
以x轴非负半轴为极轴，取相同单位长度)中，曲线C的极坐标方程为
.
(1)写出直线l的参数方程，并将曲线C的方程化为直角坐标方程；
(2)若曲线C与直线相交于不同的两点M，N，求|PM|＋|PN|的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为正整数，数列
满足
，
，设数列
满足
.
（1）求证：数列
为等比数列；
（2）若数列是等差数列，求实数
的值；
（3）若数列是等差数列，前项和为
，对任意的
，均存在
，使得
成立，求满足条件的所有整数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如：
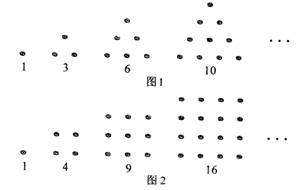
他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…这样的数为正方形数.下列数中既是三角形数又是正方形数的是（ ）
A. 36 B. 45 C. 99 D. 100
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝x2＋
(x≠0，a∈R)．
(1)判断函数f(x)的奇偶性；
(2)若f(x)在区间[2，＋∞)上是增函数，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com