
北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为 分,规定测试成绩在
分,规定测试成绩在 之间为体质优秀;在
之间为体质优秀;在 之间为体质良好;在
之间为体质良好;在 之间为体质合格;在
之间为体质合格;在 之间为体质不合格.
之间为体质不合格.
现从某校高三年级的 名学生中随机抽取
名学生中随机抽取 名学生体质健康测试成绩,其茎叶图如下:
名学生体质健康测试成绩,其茎叶图如下:

(Ⅰ)试估计该校高三年级体质为优秀的学生人数;
(Ⅱ)根据以上 名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取
名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取 名学生,再从这
名学生,再从这 名学生中选出
名学生中选出 人.
人.
(ⅰ)求在选出的 名学生中至少有
名学生中至少有 名体质为优秀的概率;
名体质为优秀的概率;
(ⅱ)求选出的 名学生中体质为优秀的人数不少于体质为良好的人数的概率.
名学生中体质为优秀的人数不少于体质为良好的人数的概率.
(Ⅰ)100;(Ⅱ)(ⅰ) ,(ⅱ)
,(ⅱ)
【解析】
试题分析:(Ⅰ)由茎叶图可知抽取的30名学生中体质优秀的有10人,所以优秀率为 ,用总数乘以优秀率即可得优秀的总人数。(Ⅱ)由茎叶图可知抽取的30名学生中体质优秀的有10人,体质为良好的15人。所以样本中体质为优秀和良好的学生的比为
,用总数乘以优秀率即可得优秀的总人数。(Ⅱ)由茎叶图可知抽取的30名学生中体质优秀的有10人,体质为良好的15人。所以样本中体质为优秀和良好的学生的比为 。分层抽样的特点是在各层按比例抽取,所以抽取的5人中有3人体质为良好有2人体质为优秀。(ⅰ)和(ⅱ)中的概率均属古典概型,用例举法分别求基本事件总数和所求事件包含的基本事件数即可。
。分层抽样的特点是在各层按比例抽取,所以抽取的5人中有3人体质为良好有2人体质为优秀。(ⅰ)和(ⅱ)中的概率均属古典概型,用例举法分别求基本事件总数和所求事件包含的基本事件数即可。
试题解析:解:(Ⅰ)根据抽样,估计该校高三学生中体质为优秀的学生人数有 人. 3分
人. 3分
(Ⅱ)依题意,体质为良好和优秀的学生人数之比为  .
.
所以,从体质为良好的学生中抽取的人数为 ,从体质为优秀的学生中抽取的人数为
,从体质为优秀的学生中抽取的人数为 . 6分
. 6分
(ⅰ)设在抽取的 名学生中体质为良好的学生为
名学生中体质为良好的学生为 ,
, ,
, ,体质为优秀的学生为
,体质为优秀的学生为 ,
, .
.
则从 名学生中任选
名学生中任选 人的基本事件有
人的基本事件有 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 个,其中“至少有
个,其中“至少有 名学生体质为优秀”的事件有
名学生体质为优秀”的事件有 ,
, ,
, ,
, ,
, ,
, ,
, ,
,  ,
,
 个.
个.
所以在选出的 名学生中至少有
名学生中至少有 名学生体质为优秀的概率为
名学生体质为优秀的概率为 . 10分
. 10分
(ⅱ)“选出的 名学生中体质为优秀的人数不少于体质为良好的人数”的事件有
名学生中体质为优秀的人数不少于体质为良好的人数”的事件有 ,
, ,
,
 个.
个.
所以选出的 名学生中体质为优秀的人数不少于体质为良好的人数的概率为
名学生中体质为优秀的人数不少于体质为良好的人数的概率为 .13分
.13分
考点:1分层抽样;2古典概型.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
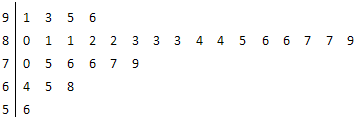
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com