
【题目】已知椭圆E:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]()
![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 设直线
设直线![]() 与椭圆E交于A、B两点,与x轴、y轴分别交于C、D两点
与椭圆E交于A、B两点,与x轴、y轴分别交于C、D两点![]() 且C、D在A、B之间或同时在A、B之外
且C、D在A、B之间或同时在A、B之外![]() 问:是否存在定值k,使得
问:是否存在定值k,使得![]() 的面积与
的面积与![]() 的面积总相等,若存在,求k的值,并求出实数m取值范围;若不存在,说明理由.
的面积总相等,若存在,求k的值,并求出实数m取值范围;若不存在,说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为素数作出判断.算法:第一步:判断n是否等于2.若______,则_______;若______,则执行第二步;第二步:依次从_______是不是n的因数,若有_________,则n不是_________数;若_______,则n____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身倡导全民做到每天参加一次以上的体育健身活动,旨在全面提高国民体质和健康水平.某市的体育部门对某小区的4000人进行了“运动参与度”统计评分(满分100分),得到了如下的频率分布直方图:
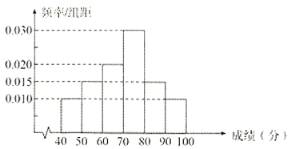
(1)求这4000人的“运动参与度”的平均得分![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为这4000人的“运动参与度”的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() ,
,![]() 分别取平均得分
分别取平均得分![]() 和方差
和方差![]() ,那么选取的4000人中“运动参与度”得分超过84.81分(含84.81分)的人数估计有多少人?
,那么选取的4000人中“运动参与度”得分超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用这4000人得分的情况来估计全市所有人的得分情况,现从全市随机抽取4人,记“运动参与度”的得分不超过84.81分的人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ,
,![]() ;②
;②![]() ,则
,则![]() ,
,![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班教室桌椅6排7列,有40名同学.空出最后一排的某两个位置,其余人按身高和视力排座位.班中有24人身高高,有18人视力好,其中,有6名同学同时具备此两个条件.已知若一名同学个子矮视力又不好,则他必须坐在前三排;若一名同学个子高视力又好,则他必须坐在最后三排.设排座位的方法是![]() ,则
,则![]() 的质因数分解中的2的次数是______.
的质因数分解中的2的次数是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国全力抗击“新冠疫情”对全球做出了巨大贡献,广大中小学生在这场“战疫”中也通过各种方式作出了贡献.某校团委准备组织一次“网上战疫”的宣传活动,活动包含4项子活动.现随机抽取了5个班级中的25名同学进行关于活动方案的问卷调查,其中关于4项子活动的赞同情况统计如下:
班级代码 | A | B | C | D | E | 合计 |
4项子活动全部赞同的人数 | 3 | 4 | 8 | 3 | 2 | 20 |
4项子活动不全部赞同的人数 | 1 | 1 | 0 | 2 | 1 | 5 |
合计问卷调查人数 | 4 | 5 | 8 | 5 | 3 | 25 |
现欲针对4项子活动的活动内容作进一步采访调研,每项子活动采访1名学生.
(1)若每项子活动都从这25名同学中随机选取1人采访,求4次采访中恰有1次采访的学生对“4项子活动不全部赞同”的概率;
(2)若从A班和E班的被问卷调查者中各随机选取2人作为采访调研的对象,记选取的4人中“4项子活动全部赞同”的人数为X,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果![]() 不是等差数列,但若
不是等差数列,但若![]() ,使得
,使得![]() ,那么称
,那么称![]() 为“局部等差”数列.已知数列
为“局部等差”数列.已知数列![]() 的项数为4,记事件
的项数为4,记事件![]() :集合
:集合![]() ,事件
,事件![]() :
:![]() 为“局部等差”数列,则条件概率
为“局部等差”数列,则条件概率![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校初中部共120名教师,高中部共180名教师,其性别比例如图所示,已知按分层抽样方法得到的工会代表中,高中部女教师有6人,则工会代表中男教师的总人数为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com