
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中
万元,其中![]() .
.
(1)若设备升级后生产这批![]() 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批![]() 产品的利润,求
产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批![]() 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批![]() 产品的利润,求
产品的利润,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】已知{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110,且a1,a2,a4成等比数列。
(1)证明:a1=d;
(2)求公差d的值和数列{an}的通项公式。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=2x-3-1的图象,只需把函数y=2x的图象上所有的点( )
A. 向右平移3个单位长度,再向下平移1个单位长度
B. 向左平移3个单位长度,再向下平移1个单位长度
C. 向右平移3个单位长度,再向上平移1个单位长度
D. 向左平移3个单位长度,再向上平移1个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l、m 、n 与平面α、β给出下列四个命题:
①若m∥l,n∥l,则m∥n; ②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;④若m⊥β,α⊥β,则m∥α
其中,假命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中
万元,其中![]() .
.
(1)若设备升级后生产这批![]() 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批![]() 产品的利润,求
产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批![]() 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批![]() 产品的利润,求
产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的焦距为2,离心率为
的焦距为2,离心率为![]() ,
,![]() 轴上一点
轴上一点![]() 的坐标为
的坐标为![]() .
.
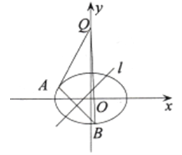
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求
,求
实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
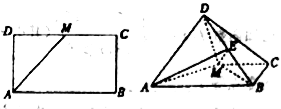
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在何位置时,三棱锥
在何位置时,三棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 的体积之比为1:3?
的体积之比为1:3?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com