
【题目】如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.
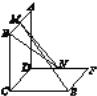
【答案】(1) ![]() .(2) 见解析.
.(2) 见解析.
【解析】(1)解:取CD的中点G,
连结MG,NG.

因为四边形ABCD,DCEF为正方形,
且边长为2,
所以MG⊥CD,MG=2,NG=![]() .
.
因为平面ABCD⊥平面DCEF,
所以MG⊥平面DCEF.可得MG⊥NG.
所以MN=![]() =
=![]() .
.
(2)证明:假设直线ME与BN共面,
则AB平面MBEN,且平面MBEN与平面DCEF交于EN.
由题意知两正方形不共面,故AB平面DCEF.
又AB∥CD,所以AB∥平面DCEF,
而EN为平面MBEN与平面DCEF的交线,
所以AB∥EN.
又AB∥CD∥EF,所以EN∥EF,
这与EN∩EF=E矛盾,故假设不成立.
所以ME与BN不共面,它们是异面直线.


科目:高中数学 来源: 题型:
【题目】![]() 年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从
年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从![]() 年下半年的会员中随机调查了
年下半年的会员中随机调查了![]() 个会员,得到会员对售后服务的满意度评分如下:
个会员,得到会员对售后服务的满意度评分如下:
![]()
根据会员满意度评分,将会员的满意度从低到高分为三个等级:
满意度评分 | 低于 |
| 不低于 |
满意度等级 | 不满意 | 比较满意 | 非常满意 |
(1)根据这![]() 个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
(2)以(1)中的频率作为概率,假设每个会员的评价结果相互独立.
(i)若从下半年的所有会员中随机选取![]() 个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
(ii)若从下半年的所有会员中随机选取![]() 个会员,记评分非常满意的会员的个数为
个会员,记评分非常满意的会员的个数为![]() ,求
,求![]() 的分布列,数学期望
的分布列,数学期望![]() 及方差
及方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数)
为参数)
(1)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)当![]() (
(![]() )时在曲线
)时在曲线![]() 上对应的点为
上对应的点为![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的极坐标,并判断
点的极坐标,并判断![]() 是否在曲线
是否在曲线![]() 上(其中点
上(其中点![]() 为半圆的圆心)
为半圆的圆心)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为y=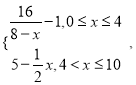 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(1≤a≤4)个单位的药剂,要使接下来的4天中能够持续有效净化,试求a的最小值(精确到0.1,参考数据: ![]() 取1.4).
取1.4).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.

(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·贵州适应性考试)如图,在正方体ABCDA1B1C1D1中,点P是线段A1C1上的动点,则三棱锥PBCD 的俯视图与正视图面积之比的最大值为( )

A. 1 B. ![]()
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
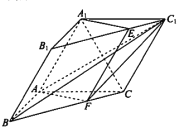
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)记四棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com