
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
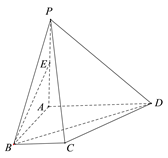
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(i)过点![]() 作一直线
作一直线![]() 与
与![]() 平行,在图中画出直线
平行,在图中画出直线![]() 并说明理由;
并说明理由;
(ii)求平面![]() 将三棱锥
将三棱锥![]() 分成的两部分体积的比.
分成的两部分体积的比.
科目:高中数学 来源: 题型:
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段![]() 的长度为
的长度为![]() ,在线段
,在线段![]() 上取两个点
上取两个点![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 为一边在线段
为一边在线段![]() 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段![]() ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段![]() 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:

记第![]() 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为![]() ,现给出有关数列
,现给出有关数列![]() 的四个命题:
的四个命题:
①数列![]() 是等比数列;
是等比数列;
②数列![]() 是递增数列;
是递增数列;
③存在最小的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() ;
;
④存在最大的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() .
.
其中真命题的序号是________________(请写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 与椭圆
与椭圆![]() 的离心率相同.
的离心率相同.

(1)求![]() 的值;
的值;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,交椭圆
,交椭圆![]() 于另一点
于另一点![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在
在![]() 之间).①求
之间).①求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点);②设
为坐标原点);②设![]() 的中点为
的中点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,试探究点
,试探究点![]() 是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元,若购买6台A型台灯和2台B型台灯共需470元.
(1)求A、B两种型号台灯每台分别多少元?
(2)采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com