
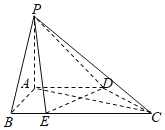
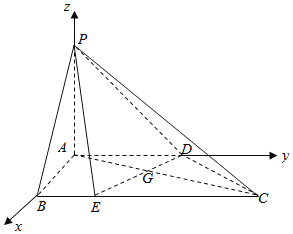
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点且
上一点且![]() =
=![]() =
=![]() =
=![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由平面![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,从而可得
,从而可得![]() ,分别以
,分别以![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,计算可得
,计算可得![]() ,从而可证
,从而可证![]() 平面
平面![]() ,即得所要证明的面面垂直.
,即得所要证明的面面垂直.
(2)设![]() ,可由直线
,可由直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() 得到
得到![]() ,再求出平面
,再求出平面![]() 的一个法向量后利用数量积可求法向量的夹角的余弦值,从而得到二面角的余弦值.
的一个法向量后利用数量积可求法向量的夹角的余弦值,从而得到二面角的余弦值.
(1)证明:∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() =
=![]() ,
,
![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,故
,故![]() .又
.又![]() .
.
分别以![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,
轴,
建立空间直角坐标系![]() ,不妨设
,不妨设![]() ,
,
可得![]() ,
,
设![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
由![]() ,
,![]() ,
,
∴![]() 且
且![]() ,
,
∵![]() 、
、![]() 是平面
是平面![]() 内的相交直线,∴
内的相交直线,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)由(1)得平面![]() 的一个法向量是
的一个法向量是![]() ,
,![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则![]() =
=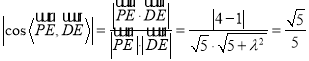 ,
,
解得![]() .∵
.∵![]() ,∴
,∴![]() ,可得
,可得![]() 的坐标为
的坐标为![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,
由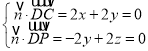 ,令
,令![]() =
=![]() ,得
,得![]() .
.
∴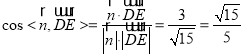 .
.
由图形可得二面角![]() 的平面角是锐角,
的平面角是锐角,
∴ 二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】如图,某森林公园内有一条宽为100米的笔直的河道(假设河道足够长),现拟在河道内围出一块直角三角形区域养殖观赏鱼.三角形区域记为![]() ,
,![]() 到河两岸距离
到河两岸距离![]() ,
,![]() 相等,
相等,![]() ,
,![]() 分别在两岸上,
分别在两岸上,![]() .为方便游客观赏,拟围绕
.为方便游客观赏,拟围绕![]() 区域在水面搭建景观桥.为了使桥的总长度
区域在水面搭建景观桥.为了使桥的总长度![]() (即
(即![]() 的周长)最短,工程师设计了以下两种方案:
的周长)最短,工程师设计了以下两种方案:
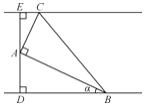
方案1:设![]() ,求出
,求出![]() 关于
关于![]() 的函数解析式
的函数解析式![]() ,并求出
,并求出![]() 的最小值.
的最小值.
方案2:设![]() 米,求出
米,求出![]() 关于
关于![]() 的函数解析式
的函数解析式![]() ,并求出
,并求出![]() 的最小值.
的最小值.
请从以上两种方案中自选一种解答.(注:如果选用了两种解答方案,则按第一种解答计分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
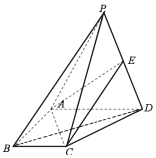
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C1的参数方程为
中,曲线C1的参数方程为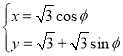 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)已知曲线C3的极坐标方程为![]() ,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,A、B均异于原点O,且
,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,A、B均异于原点O,且![]() ,求实数α的值.
,求实数α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系,从若干个高中男学生中抽取了1000个样本,得到如下数据.
数据一:身高在![]() (单位:
(单位:![]() )的体重频数统计
)的体重频数统计
体重 ( |
|
|
|
|
|
|
|
|
人数 | 20 | 60 | 100 | 100 | 80 | 20 | 10 | 10 |
数据二:身高所在的区间含样本的个数及部分数据
身高 |
|
|
|
|
|
平均体重
| 45 | 53.6 | 60 | 75 |
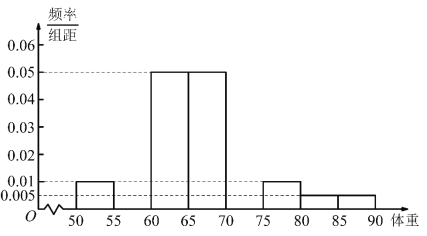
(1)依据数据一将上面男高中生身高在![]() (单位:
(单位:![]() )体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在
)体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在![]() (单位:
(单位:![]() )的中学生的平均体重;(保留小数点后一位)
)的中学生的平均体重;(保留小数点后一位)
(2)依据数据一、二,计算身高(取值为区间中点)和体重的相关系数约为0.99,能否用线性回归直线来刻画中学生身高与体重的相关关系,请说明理由;若能,求出该回归直线方程;
(3)说明残差平方和或相关指数![]() 与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
参考公式: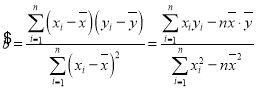 ,
,![]() .
.
参考数据:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为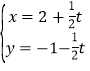 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,右准线为
,右准线为![]() .点
.点![]() 是椭圆
是椭圆![]() 上异于长轴端点的任意一点,连接
上异于长轴端点的任意一点,连接![]() 并延长交椭圆
并延长交椭圆![]() 于点
于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且直线
为坐标原点,且直线![]() 与右准线
与右准线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)试确定直线![]() 与椭圆
与椭圆![]() 的公共点的个数,并说明理由.
的公共点的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为改善环境,节约资源,我国自2019年起在全国地级及以上城市全面启动生活垃圾分类,垃圾分类已成为一种潮流.某市一小区的主管部门为了解居民对垃圾分类的认知是否与其受教育程度有关,对该小区居民进行了随机抽样调查,得到如下统计数据的列联表:
知道如何对垃圾进行分类 | 不知道如何对垃圾进行分类 | 合计 | |
未受过高等教育 |
| 10 |
|
受过高等教育 |
|
|
|
合计 |
|
| 50 |
(1)求列联表中的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率;
的值,并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率;
(2)根据列联表判断能否有![]() 的把握认为该小区居民对垃圾分类的认知与其受教育程度有关?
的把握认为该小区居民对垃圾分类的认知与其受教育程度有关?
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
|
|
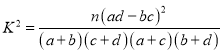 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com