
【题目】如图,四棱锥S﹣ABCD中,M是SB的中点,AB∥CD,BC⊥CD,且AB=BC=2,CD=SD=1,又SD⊥面SAB.
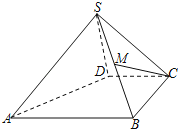
(1)证明:CD⊥SD;
(2)证明:CM∥面SAD;
(3)求四棱锥S﹣ABCD的体积.
【答案】(1)证明见解析 (2)证明见解析(3)![]() .
.
【解析】
(1)由![]() 平面
平面![]() 证得
证得![]() ,结合
,结合![]() ,证得
,证得![]()
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,通过证明四边形
,通过证明四边形![]() 是平行四边形,证得
是平行四边形,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(3)通过求![]() ,结合
,结合![]() ,求得四棱锥
,求得四棱锥![]() 的体积.
的体积.
(1)证明:由SD⊥面SAB,AB面SAB,
所以SD⊥AB,又AB∥CD,
所以CD⊥SD;
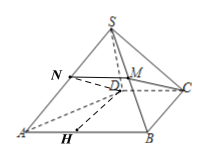
(2)取SA中点N,连接ND,NM,
则NM∥AB,且MN![]() ,AB∥CD,
,AB∥CD,
所以NMCD是平行四边形,
ND∥MC,且ND平面SAD,MC平面SAD,
所以CM∥面SAD;
(3)VS﹣ABCD:VS﹣ABD=SABCD:S△ABD=3:2,
过D作DH⊥AB,交于H,由题意得,BD=AD![]() ,
,
在Rt△DSA,Rt△DSB中,SA=SB![]() 2.
2.
所以,![]() ,/span>
,/span>
四棱锥S﹣ABCD的体积为:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=![]() x上时,求直线AB的方程.
x上时,求直线AB的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(1)证明|EA|+|EB|为定值,并写出点E的轨迹方程;
(2)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大豆,古称菽,原产中国,在中国已有五千年栽培历史。皖北多平原地带,黄河故道土地肥沃,适宜种植大豆。2018年春,为响应中国大豆参与世界贸易的竞争,某市农科院积极研究,加大优良品种的培育工作。其中一项基础工作就是研究昼夜温差大小与大豆发芽率之间的关系。为此科研人员分别记录了5天中每天100粒大豆的发芽数得如下数据表格:
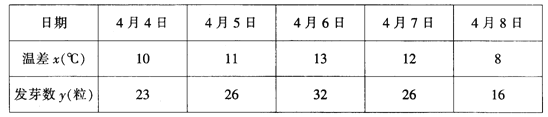
科研人员确定研究方案是:从5组数据中选3组数据求线性回归方程,再用求得的回归方程对剩下的2组数据进行检验.
(1)求剩下的2组数据恰是不相邻的2天数据的概率;
(2)若选取的是4月5日、6日、7日三天数据据此求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与实际数据的误差绝对值均不超过1粒,则认为得到的线性回归方程是可靠的,请检验(Ⅱ)中回归方程是否可靠?
注: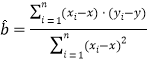
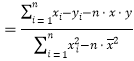 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区的各景点从2009年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是从2009年至2018年,该景点的旅游人数![]() (万人)与年份
(万人)与年份![]() 的数据:
的数据:
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
旅游人数 | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
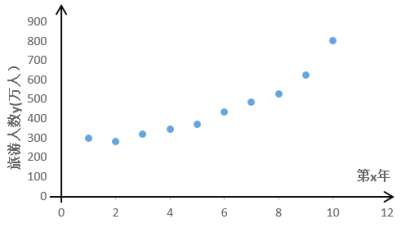
该景点为了预测2021年的旅游人数,建立了![]() 与
与![]() 的两个回归模型:
的两个回归模型:
模型①:由最小二乘法公式求得![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近.
的附近.
(1)根据表中数据,求模型②的回归方程![]() .(
.(![]() 精确到个位,
精确到个位,![]() 精确到0.01).
精确到0.01).
(2)根据下列表中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
回归方程 | ① | ② |
| 30407 | 14607 |
参考公式、参考数据及说明:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为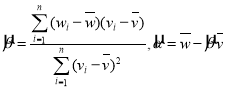 .②刻画回归效果的相关指数
.②刻画回归效果的相关指数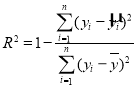 ;③参考数据:
;③参考数据:![]() ,
,![]() .
.
|
|
|
|
|
|
5.5 | 449 | 6.05 | 83 | 4195 | 9.00 |
表中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边长分别为a,b,c,且满足a2+c2-b2=![]() ac.
ac.
(1)求角B的大小;
(2)若2bcos A=![]() (ccosA+acosC),BC边上的中线AM的长为
(ccosA+acosC),BC边上的中线AM的长为![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 图象上不同两点
图象上不同两点![]() ,
,![]() 处切线的斜率分别是
处切线的斜率分别是![]() ,
,![]() 规定
规定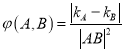 (
(![]() 为线段
为线段![]() 的长度)叫做曲线
的长度)叫做曲线![]() 在点
在点![]() 与
与![]() 之间的“平方弯曲度”,给出以下命题:
之间的“平方弯曲度”,给出以下命题:
①函数![]() 图象上两点
图象上两点![]() 与
与![]() 的横坐标分别为1和2,则
的横坐标分别为1和2,则![]() ;
;
②存在这样的函数,图象上任意两点之间的“平方弯曲度”为常数;
③设点![]() ,
,![]() 是抛物线
是抛物线![]() 上不同的两点,则
上不同的两点,则![]() ;
;
④设曲线![]() (
(![]() 是自然对数的底数)上不同两点
是自然对数的底数)上不同两点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最大值为
的最大值为![]() .
.
其中真命题的序号为__________(将所有真命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com