
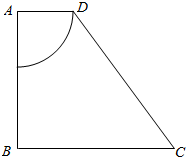
 如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.
如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S. 分析 根据题意,得出该几何体是一个圆台挖去半个球,结合图中数据求出它的体积与表面积.
解答 解:该几何体是由一个圆台挖去半个球,(2 分)
由题意知,该圆台的上下底面的半径分别为2和5,高为4,母线为5,(4 分)
挖去半球的半径为2; (5 分)
所以该几何体的体积为
V=$\frac{1}{3}$π(22+52+2×5)×4-$\frac{1}{2}$×$\frac{4π}{3}$×23=52π-$\frac{16π}{3}$=$\frac{140π}{3}$;(8分)
该几何的表面积为
S=π×52+π(5+2)×5+$\frac{1}{2}$×4×π×22=68π.(12分)
点评 本题考查了空间几何体的表面积与体积的应用问题,是基础题目.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:解答题
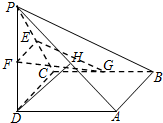 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1,-1) | B. | (-i,j,-k) | C. | (1,-1,-1) | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 75 | B. | 65 | C. | 60 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com