Question

14．已知一个上、下底面为正三角形且两底面中心连线垂直于底面的三棱台的两底面边长分别为20cm和30cm，且其侧面积等于两底面面积之和，求棱台的高．

Answer 1

分析 利用棱台的高、斜高、边心距构成直角梯形，通过构造直角三角形，利用勾股定理求出棱台的高．

解答 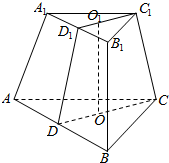解：如图所示，
在正三棱台ABC-A₁B₁C₁中，
两底面边长分别为AB=30cm，A₁B₁=20cm，
∴侧面积为S_侧=3×$\frac{1}{2}$×（30+20）•DD₁，
两底面积之和为S_底=$\frac{\sqrt{3}}{4}$×（30²+20²），
∵S_侧=S_底，
∴$\frac{3×50}{2}$•DD₁=$\frac{\sqrt{3}}{4}$×1300，
解得DD₁=$\frac{13\sqrt{3}}{3}$，
∴OO₁²=$（\frac{13\sqrt{3}}{3}）^{2}-（\frac{\sqrt{3}}{2}×30×\frac{1}{3}-\frac{\sqrt{3}}{2}×20×\frac{1}{3}）^{2}$=$\frac{144}{3}$，
∴OO₁=4$\sqrt{3}$；
即棱台的高为4$\sqrt{3}$．

点评 本题考查了求正三棱台的高的问题，解题时应画出图形，结合图形解答问题，是计算题目．