
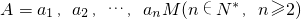 ,若a1+a2+…+an=a1a2…an,则称集合A是集合M的n元“好集”.
,若a1+a2+…+an=a1a2…an,则称集合A是集合M的n元“好集”. =(-1)×
=(-1)× ,∴
,∴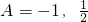 .
.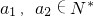 ,不妨设a2>a1
,不妨设a2>a1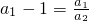 ,∵
,∵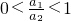 ,
,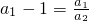 的a1∈N*不存在;
的a1∈N*不存在;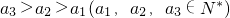 ,
, }符合条件求解(1);
}符合条件求解(1);

科目:高中数学 来源:2012-2013学年上海市闵行区七宝中学高一(上)周考数学试卷(解析版) 题型:解答题
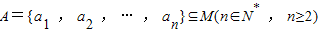 ,若a1+a2+…+an=a1a2…an,则称集合A是集合M的n元“好集”.
,若a1+a2+…+an=a1a2…an,则称集合A是集合M的n元“好集”.查看答案和解析>>
科目:高中数学 来源:2012年福建省厦门市高三3月质量检查数学试卷(理科)(解析版) 题型:选择题
 ,若a1+a2+…+an=63,则展开式中系数最大的项是( )
,若a1+a2+…+an=63,则展开式中系数最大的项是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com