
若正数项数列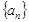 的前
的前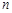 项和为
项和为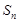 ,首项
,首项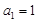 ,点
,点 ,
,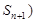 在曲线
在曲线 上.
上.
(1)求 ,
,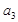 ;
;
(2)求数列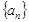 的通项公式
的通项公式 ;
;
(3)设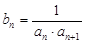 ,
, 表示数列
表示数列 的前项和,若
的前项和,若 恒成立,求
恒成立,求 及实数
及实数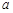 的取值范围.
的取值范围.
(1) ;(2)
;(2)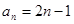 ;(3)
;(3) .
.
解析试题分析:(1)根据已知点 ,
,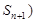 在曲线
在曲线 上,代入曲线,得到
上,代入曲线,得到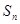 与
与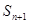 的关系,再根据
的关系,再根据 ,分别取
,分别取 和
和 代入关系式,得到关于
代入关系式,得到关于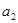 与
与 的方程组,解方程,得到结果;(2)由(1)得的
的方程组,解方程,得到结果;(2)由(1)得的 ,因为是正项数列,所以两边开方,得
,因为是正项数列,所以两边开方,得 与
与 的地推关系式,从而判定数列形式,得出
的地推关系式,从而判定数列形式,得出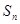 的通项公式,再根据
的通项公式,再根据
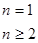 ,得出
,得出 的通项公式;(3)代入
的通项公式;(3)代入 的通项公式得到
的通项公式得到 ,然后裂项,经过裂项相消,得到
,然后裂项,经过裂项相消,得到 的前项和
的前项和 ,,通过分离常数可以判定
,,通过分离常数可以判定 的单调性,求出最值,若
的单调性,求出最值,若 恒成立,那么
恒成立,那么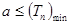 ,得到的范围.此题计算相对较大,属于中档题.
,得到的范围.此题计算相对较大,属于中档题.
试题解析:(1)解:因为点 ,
,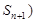 在曲线
在曲线 上,所以
上,所以 .
.
分别取 和
和 ,得到
,得到 ,
,
由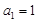 解得
解得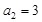 ,
,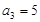 . 4分
. 4分
(2)解:由 得
得 .
.
数列 是以
是以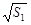 为首项,
为首项, 为公差的等差数列,所以
为公差的等差数列,所以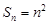 , 6分
, 6分
由
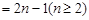 ,当
,当 时,
时, ,
,
所以 . 8分
. 8分
(3)解:因为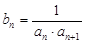

 ,
,
所以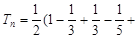

 , 11分
, 11分
显然 是关于
是关于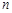 的增函数, 所以
的增函数, 所以 有最小值
有最小值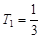 ,
,
因为 恒成立,所以
恒成立,所以 ,
,
因此 ,实数
,实数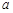 的取值范围是
的取值范围是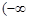 ,
,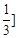 . 13分
. 13分
考点:1.等差数列的定义;2.已知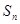 求
求 ;3.裂项相消;4.函数最值.
;3.裂项相消;4.函数最值.


科目:高中数学 来源: 题型:解答题
设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1cos x-an+2sin x满足f′ =0.
=0.
(1)求数列{an}的通项公式;
(2)若bn=2(an+ ),求数列{bn}的前n项和Sn.
),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an}满足a1=1,an-an-1+2anan-1=0(n∈N*,n>1).
(1)求证:数列 是等差数列并求数列{an}的通项公式;
是等差数列并求数列{an}的通项公式;
(2)设bn=anan+1,求证:b1+b2+…+bn< 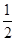 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知首项为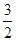 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-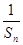 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设无穷数列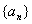 的首项
的首项 ,前
,前 项和为
项和为 (
( ),且点
),且点 在直线
在直线 上(
上(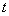 为与
为与 无关的正实数).
无关的正实数).
(1)求证:数列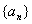 (
( )为等比数列;
)为等比数列;
(2)记数列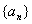 的公比为
的公比为 ,数列
,数列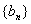 满足
满足 ,设
,设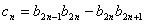 ,求数列
,求数列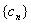 的前
的前 项和
项和 ;
;
(3)(理)若(1)中无穷等比数列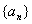 (
( )的各项和存在,记
)的各项和存在,记 ,求函数
,求函数 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知n∈N*,数列{dn}满足dn=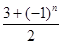 ,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,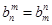 .
.
(1)求数列{an}和数列{bn}的通项公式;
(2)将数列{bn}中的第a1项,第a2项,第a3项,…,第an项,…删去后,剩余的项按从小到大的顺序排成新数列{cn},求数列{cn}的前2 013项和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
大学生自主创业已成为当代潮流。长江学院大三学生夏某今年一月初向银行贷款20000元作开店资金,全部用作批发某种商品,银行贷款的年利率为6%,约定一年后一次还清贷款。已知夏某每月月底获得的利润是该月月初投人资金的15%,每月月底需要交纳个人所得税为该月所获利润的20%,当月房租等其他开支1500元,余款作为资金全部投入批发该商品再经营,如此继续,假定每月月底该商品能全部卖出。
(1)设夏某第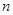 个月月底余
个月月底余 元,第
元,第 个月月底余
个月月底余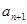 元,写出
元,写出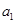 的值并建立
的值并建立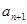 与
与 的递推关系式;
的递推关系式;
(2)预计年底夏某还清银行贷款后的纯收入。(参考数据:1.1211≈3.48,1.1212≈3.90,0.1211≈7.43×10﹣11,0.1212≈8.92×10﹣12)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com