
分析 (1)求得$\sqrt{x}$-x原函数,根据定积分的运算,即可求得;
(2)由$\int_1^2{\;}({2^x}+\frac{1}{x})dx$=($\frac{{2}^{x}}{ln2}$+lxx)${丨}_{1}^{2}$,代入即可求得答案;
(3)由复合函数的求原式的公式可知sin2x的原函数为-$\frac{1}{2}$cos2x,代入即可求得结果.
解答 解:(1)$\int_1^4{\sqrt{x}}(1-\sqrt{x})dx$=${∫}_{1}^{4}$($\sqrt{x}$-x)dx=($\frac{2}{3}$${x}^{\frac{3}{2}}$-$\frac{1}{2}$x2)${丨}_{1}^{4}$=-$\frac{17}{6}$;
(2)$\int_1^2{\;}({2^x}+\frac{1}{x})dx$=($\frac{{2}^{x}}{ln2}$+lnx)${丨}_{1}^{2}$=($\frac{{2}^{2}}{ln2}$+ln2)-($\frac{{2}^{1}}{ln2}$+ln1)=$\frac{2}{ln2}$+ln2,
(3)$\int_0^{\frac{Π}{3}}{\;}(sinx-sin2x)dx$=(-cosx+$\frac{1}{2}$cos2x)${丨}_{0}^{\frac{π}{3}}$=(-$\frac{1}{2}$-$\frac{1}{4}$)-(-1+$\frac{1}{2}$)=-$\frac{1}{4}$.
点评 本题考查定积分的运算,考查计算求原函数的方法,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2}{3}$ | C. | -$\frac{2}{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
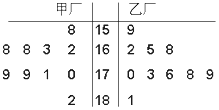 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的数据落在(164,181]的零件为优质品.现从两个分厂生产的零件中随机各抽出10件,量其内径尺寸(单位:mm),获得内径尺寸数据的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-x-1≤0 | B. | ?x∈R,x2-x-1>0 | ||
| C. | ?x0∈R,${x_0}^2-{x_0}-1≤0$ | D. | ?x0∈R,${x_0}^2-{x_0}-1≥0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com