
【题目】4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜” 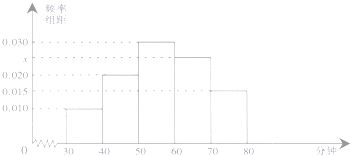
附:K2= ![]() n=a+b+c+d
n=a+b+c+d
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)求x的值并估计全校3000名学生中读书谜大概有多少?(经频率视为频率)
(2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点P(2,0),及⊙C:x2+y2﹣6x+4y+4=0.
(1)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(2)设过点P的直线与⊙C交于A、B两点,当|AB|=4,求以线段AB为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(﹣x)=8﹣f(4+x),函数g(x)= ![]() ,若函数f(x)与g(x)的图象共有168个交点,记作Pi(xi , yi)(i=1,2,…,168),则(x1+y1)+(x2+y2)+…+(x168+y168)的值为( )
,若函数f(x)与g(x)的图象共有168个交点,记作Pi(xi , yi)(i=1,2,…,168),则(x1+y1)+(x2+y2)+…+(x168+y168)的值为( )
A.2018
B.2017
C.2016
D.1008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两组数据的茎叶如图所示,若它们的平均数相同,则下列关于甲、乙两组数据稳定性的描述,正确的是( ) 
A.甲较稳定
B.乙较稳定
C.二者相同
D.无法判断
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC中角A,B,C的对边,且csinB= ![]() bcosC.
bcosC.
(1)求角C的大小;
(2)若c=3,sinA=2sinB,求△ABC的面积S△ABC .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,其离心率为
,其离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相交于
相交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为正三角形,若存在,求直线
为正三角形,若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com