Question

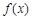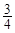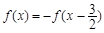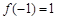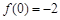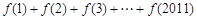已知定义在R上的函数的图象关于点（-，0）对称，且满足，，，则的值是

A．2

B．1

C．-1

D．-2

Answer 1

B

解析考点：抽象函数及其应用；函数的值．
分析：由函数图象关于点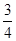（- ，0）对称，知f(x)="-f(-x-" )，由f(x)="-f(x-" )可得f（x）=f（x-3），从而f（x）=f（x+3），f（x）是最小正周期为3的周期函数；再由f(-x- )="f(x+" )，可得故f（x）是偶函数，从而结合条件可求得f（1），f（2），f（3）的值．
解：∵函数图象关于点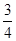（-，0）对称，
∴f(x)=-f(-x-)，①
∵f(x)=-f(x-)，即f（x-）=-f（x），
∴f[（x-）-]=-f（x-）=f（x），即f（x-3）=f（x）=f[（x-3）+3]，
∴f（x+3）=f（x）；
∴f（x）是最小正周期为3的周期函数；
又f(-x-)=f(x+)，故f（x）是偶函数．
∴f（-1）=f（2）=1，f（1）=f（-1）=1，f（3）=f（0）=-2，
∴f（1）+f（2）+f（3）=0，又f（x）是最小正周期为3的周期函数，
∴f（1）+f（2）+f（3）+…+f（2011）
=f（2011）=f（3×670+1）=f（1）=1．
故选B．