
【题目】近年来,随着![]() 网络的普及和智能手机的更新换代,各种方便的
网络的普及和智能手机的更新换代,各种方便的![]() 相继出世,其功能也是五花八门.某大学为了调查在校大学生使用
相继出世,其功能也是五花八门.某大学为了调查在校大学生使用![]() 的主要用途,随机抽取了
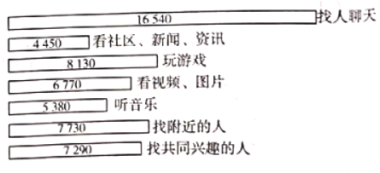
的主要用途,随机抽取了![]() 名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
①可以估计使用![]() 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
②可以估计不足![]() 的大学生使用
的大学生使用![]() 主要玩游戏;
主要玩游戏;
③可以估计使用![]() 主要找人聊天的大学生超过总数的
主要找人聊天的大学生超过总数的![]() .
.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 常数
常数![]() )满足
)满足![]() .
.
(1)求出![]() 的值,并就常数
的值,并就常数![]() 的不同取值讨论函数
的不同取值讨论函数![]() 奇偶性;
奇偶性;
(2)若![]() 在区间
在区间![]() 上单调递减,求
上单调递减,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,当![]() 取最小值时,证明:
取最小值时,证明:![]() 恰有一个零点
恰有一个零点![]() 且存在递增的正整数数列
且存在递增的正整数数列![]() ,使得
,使得![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e-x,其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围;
(3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(-![]() +3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
+3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
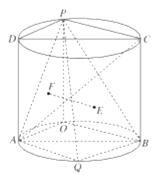
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点P是圆弧
是边长为2的正方形,点P是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点Q是圆弧
重合),点Q是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点P在平面![]() 上的射影为点O,点
上的射影为点O,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(i)证明:![]() 平面
平面![]() ;
;
(ii)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在频率分布直方图中,众数左边和右边的直方图的面积相等;
B.为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行編号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样;
C.“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
D.命题![]() :“
:“![]() ,使得
,使得![]() ”的否定为:“
”的否定为:“![]() ,均有
,均有![]() ”.
”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com