
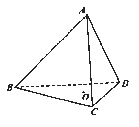
【题目】如图,在正四面体ABCD中, ![]() 是
是![]() 的中心,
的中心, ![]() 分别是
分别是![]() 上的动点,且
上的动点,且![]() .
.
(1)若![]() 平面
平面![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() ,正四面体ABCD的棱长为
,正四面体ABCD的棱长为![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角余弦值.
所成的角余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)本问主要考查线面平行性质定理的应用,若![]() 平面
平面![]() ,那么经过OE的平面与平面ACD相交,则OE平行于交线,因此需要找到经过OE的平面,由
,那么经过OE的平面与平面ACD相交,则OE平行于交线,因此需要找到经过OE的平面,由![]() 是正
是正![]() 的中心,易知O为BC的三等分点,因此能确定E点位置;(2)本问主要考查用空间向量求二面角问题,当
的中心,易知O为BC的三等分点,因此能确定E点位置;(2)本问主要考查用空间向量求二面角问题,当![]() 时,点
时,点![]() 分别是
分别是![]() 的中点,以O为原点,过O作CD的垂线为x轴,过O作BC的垂线为y轴,OA为z轴,建立空间直角直角坐标系,则易得出下列各点坐标
的中点,以O为原点,过O作CD的垂线为x轴,过O作BC的垂线为y轴,OA为z轴,建立空间直角直角坐标系,则易得出下列各点坐标![]() ,
,  ,由此求出相关向量的坐标,再分别求出平面
,由此求出相关向量的坐标,再分别求出平面![]() 和平面
和平面![]() 的法向量,根据两个平面的法向量可以求夹角的余弦,再由图观察向量成角的余弦与二面角余弦之间的关系即可.
的法向量,根据两个平面的法向量可以求夹角的余弦,再由图观察向量成角的余弦与二面角余弦之间的关系即可.
试题解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,

∵![]() 是正
是正![]() 的中心 ∴点
的中心 ∴点![]() 在
在![]() 上,且
上,且![]() ,
,
∵当![]() 时,
时,![]() 平面
平面 ![]() ,
,
∴![]() ∴
∴![]() ,即
,即![]() ,
,
∴![]() .
.
(2)当![]() 时,点
时,点![]() 分别是
分别是![]() 的中点.
的中点.
建立如图所示的空间直角坐标系![]() ,依题设
,依题设
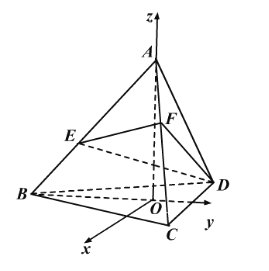
![]() ,则
,则![]() ,
,  ,
,
则 ,
,
设平面![]() 的法向量为
的法向量为![]() 则
则 ,
,
∴ ,
,
不妨令![]() ,则
,则 ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() .
.
设所求二面角为![]() ,则
,则 .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】给定椭圆![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.

(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的动点,过点
的“准圆”上的动点,过点![]() 作椭圆的切线
作椭圆的切线![]() 交“准圆”于点
交“准圆”于点![]() .
.
①当点![]() 为“准圆”与
为“准圆”与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 的方程并证明
的方程并证明![]() ;
;
②求证:线段![]() 的长为定值.
的长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所称角的最小值为45°;
④直线AB与a所称角的最小值为60°;
其中正确的是________。(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内给定三个向量 ![]() =(3,2),
=(3,2), ![]() =(﹣1,2),
=(﹣1,2), ![]() =(4,1).回答下列问题:
=(4,1).回答下列问题:
(1)若( ![]() +k
+k ![]() )∥(2
)∥(2 ![]() ﹣
﹣ ![]() ),求实数k;
),求实数k;
(2)设 ![]() =(x,y)满足(
=(x,y)满足( ![]() ﹣
﹣ ![]() )∥(
)∥( ![]() +
+ ![]() )且|
)且| ![]() ﹣
﹣ ![]() |=1,求
|=1,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过对某城市一天内单次租用共享自行车的时间![]() 分钟到
分钟到![]() 钟的
钟的![]() 人进行统计,按照租车时间
人进行统计,按照租车时间![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组做出频率分布直方图,并作出租用时间和茎叶图(图中仅列出了时间在
分组做出频率分布直方图,并作出租用时间和茎叶图(图中仅列出了时间在![]() ,
, ![]() 的数据).
的数据).

(1)求![]() 的频率分布直方图中的
的频率分布直方图中的![]() ;
;
(2)从租用时间在![]() 分钟以上(含
分钟以上(含![]() 分钟)的人数中随机抽取
分钟)的人数中随机抽取![]() 人,设随机变量
人,设随机变量![]() 表示所抽取的
表示所抽取的![]() 人租用时间在
人租用时间在![]() 内的人数,求随机变量
内的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C的坐标分别为A(4,0),B(0,4),C(3cosα,3sinα).
(1)若α∈(﹣π,0),且| ![]() |=|
|=| ![]() |,求角α的大小;
|,求角α的大小;
(2)若 ![]() ⊥
⊥ ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com