
已知函数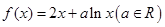 .
.
(1)讨论函数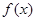 的单调性;
的单调性;
(2)若函数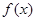 的最小值为
的最小值为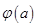 ,求
,求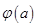 的最大值;
的最大值;
(3)若函数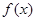 的最小值为
的最小值为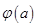 ,
,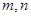 为
为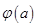 定义域
定义域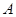 内的任意两个值,试比较
内的任意两个值,试比较 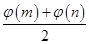 与
与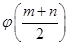 的大小.
的大小.
(1)当 时
时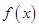 在定义域内单调递增;
在定义域内单调递增;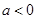 时,函数单调递减
时,函数单调递减
(2)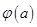 的最大值是
的最大值是
(3)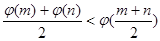
【解析】
试题分析:解: (1)显然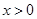 ,且
,且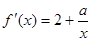 1分
1分
当 时,
时,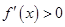 ,函数
,函数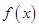 在定义域内单调递增;
在定义域内单调递增;
当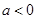 时,若
时,若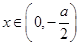 ,
,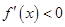 ,函数单调递减;
,函数单调递减;
若 ,
,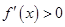 函数单调递增 4分
函数单调递增 4分
(2)由(1)知,当 时,函数
时,函数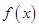 在定义域内单调递增,所以
在定义域内单调递增,所以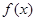 无最小值.
无最小值.
当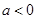 时,
时, 时,
时,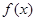 最小,即
最小,即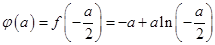
所以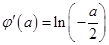
因此,当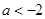 时,
时,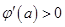 ,函数
,函数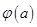 单调递增;
单调递增;
当 时,
时, ,函数
,函数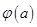 单调递减;
单调递减;
故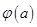 的最大值是
的最大值是 8分
8分
(3) 由(1)知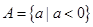 ,极小值即最小值
,极小值即最小值 ,
,
故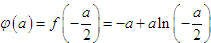
对于任意的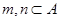 且
且 有,
有,
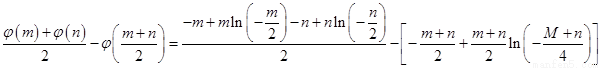
 分
分
不妨设 ,则
,则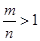 ,令
,令 则
则
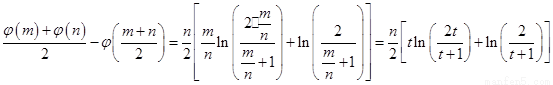
设
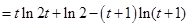
所以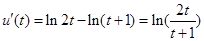 ,因为
,因为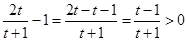
即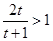 ,所以
,所以 ,即函数
,即函数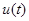 在
在 上单调递增.
上单调递增.
从而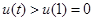 ,但是
,但是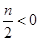 ,所以
,所以
即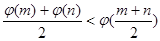 14分
14分
考点:导数的运用
点评:主要是利用导数来研究函数单调性以及函数极值的运用,属于中档题。


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com