
����Ŀ�������������������Ѿ���Ȼ�����˹��������ճ�����������ı������ǵij��з�ʽ.Ϊ�˸��õط������ڣ�ij����������˾����ٷ�![]() ���������û����۷���ϵͳ�����˽��û��Գ���״�����Żݻ�����ۣ��ִ�����ϵͳ��ѡ��
���������û����۷���ϵͳ�����˽��û��Գ���״�����Żݻ�����ۣ��ִ�����ϵͳ��ѡ��![]() ����Ϊ��ϸ��������Ϣ����ͳ�ƣ�����״�����Żݻ���۵�
����Ϊ��ϸ��������Ϣ����ͳ�ƣ�����״�����Żݻ���۵�![]() ����������:
����������:
���Żݻ���� | ���Żݻ������ | �ϼ� | |
�Գ���״������ |
|
|
|
�Գ���״�������� |
|
|
|
�ϼ� |
|
|
|
(1)�ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ�Żݻ�����복��״������֮���й�ϵ?
��ǰ������Ϊ�Żݻ�����복��״������֮���й�ϵ?
(2)Ϊ�˻����û�����˾ͨ��![]() ���û������������ȯ���û����Խ�����ȯ�������и��ѣ�Ҳ����ͨ��
���û������������ȯ���û����Խ�����ȯ�������и��ѣ�Ҳ����ͨ��![]() ת��������ij�û��������
ת��������ij�û��������![]() ������ȯ������ֻ��
������ȯ������ֻ��![]() ����һԪȯ�ָ��û�����������ȯ�����ѡȡ
����һԪȯ�ָ��û�����������ȯ�����ѡȡ![]() ��ת�������ѣ���ѡȡ��
��ת�������ѣ���ѡȡ��![]() ����������
����������![]() ����һԪȯ�ĸ���.
����һԪȯ�ĸ���.
��:������ٽ�ֵ�������ο�:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(�ο���ʽ: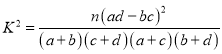 ������
������![]() )
)
���𰸡�(1) ����(2) ![]()
��������
��1���������������Լ�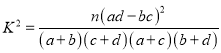 ��ʽ����������жϣ�
��ʽ����������жϣ�
��2���г�![]() ������ȯ�����ѡȡ
������ȯ�����ѡȡ![]() �ŵ����������ȷ�����������������ĸ��������ŵ��������ʵĹ�ʽ���������.
�ŵ����������ȷ�����������������ĸ��������ŵ��������ʵĹ�ʽ���������.
��(1).��![]() �����������ݣ���
�����������ݣ���
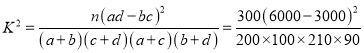
![]()
��ˣ��ڷ�����ĸ��ʲ�����![]() ��ǰ���£�
��ǰ���£�
������Ϊ�Żݻ�����복��״�������й�ϵ.
(2)![]() ��һԪȯ�ֱ��Ϊ
��һԪȯ�ֱ��Ϊ![]() ����
����![]() ����ȯ�ֱ��Ϊ
����ȯ�ֱ��Ϊ![]() .
.
���![]() ������ȯ�����ѡȡ
������ȯ�����ѡȡ![]() �ŵ��������Ϊ:
�ŵ��������Ϊ:
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��.����ѡȡ��
��.����ѡȡ��![]() ��ȯ��������
��ȯ��������
![]() ����һԪȯ��Ϊ�¼�
����һԪȯ��Ϊ�¼�![]() �����¼�
�����¼�![]() �����Ļ����¼�����Ϊ
�����Ļ����¼�����Ϊ![]() ��
��
![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]()
![]() ����������Ϊ
����������Ϊ![]() ,
,![]() ,����Ϊ
,����Ϊ![]() ,ֱ��
,ֱ��![]() :
:![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ,
,![]() ����,
����,![]() ��
Ϊ��![]() ���е�.
���е�.
��1������Բ�ı�����;
��2����ֱ��![]() :
:![]() ����Բ
����Բ![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() ,
,![]() ,
,![]() ,��
,��![]() ��
��![]() Ϊ����ԭ�㣩,��
Ϊ����ԭ�㣩,��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵķ���ȡ֮��������֮����.�����ǜ[����Դ��Ҳ�ǿ�������Դ.������������ڷ�չ�������磬��10������ȫ����������ۼ�װ�����������������й����Ƿ�չѸ�ͣ�2014���ۼ�װ��������ͻ����![]() ���ﵽ
���ﵽ![]() ���й��ķ������缼��Ҳ������죬��ȫ��Χ����Դ���������ж������ֳ�����ĵ��������.�����ǽ�10��ȫ����������ۼ�װ���������й�����װ������ͼ. ����������Ϣ����ȷ��ͳ�ƽ����ǣ� ��
���й��ķ������缼��Ҳ������죬��ȫ��Χ����Դ���������ж������ֳ�����ĵ��������.�����ǽ�10��ȫ����������ۼ�װ���������й�����װ������ͼ. ����������Ϣ����ȷ��ͳ�ƽ����ǣ� ��
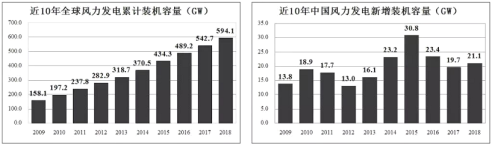
A.��ֹ��2015���й��ۼ�װ�������ﵽ��ֵ
B.10����ȫ������װ��������������
C.10�����й�����װ������ƽ������![]()
D.��ֹ��2015���й��ۼ�װ��������ȫ���ۼ�װ��������ռ�ȳ���![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����
����![]() ��������Ϊ
��������Ϊ![]() ��
��![]() Ϊ����ԭ�㣮
Ϊ����ԭ�㣮
��1������Բ![]() �ı����̣�
�ı����̣�
��2����![]() Ϊ��Բ
Ϊ��Բ![]() �ϵ����㣬
�ϵ����㣬![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����
����![]() ���е�ǡΪ��
���е�ǡΪ��![]() ʱ���ж�
ʱ���ж�![]() ������Ƿ�Ϊ��������˵�����ɣ�
������Ƿ�Ϊ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ������̬������չ�����Ѿ���������,�⽫�ƶ�����Դ������ҵ��Ѹ�ٷ�չ.�±��ǽ������ҹ�ij��������Դ���ó���������������ݵ�ͳ�Ʊ���
��� | 2014 | 2015 | 2016 | 2017 | 2018 |
��������̨�� | 8 | 10 | 13 | 25 | 24 |
ij���������˸õ���30λ�����������Ա��빺������������õ��IJ����������±���ʾ��
���ô�ͳȼ�ͳ� | ��������Դ�� | �ܼ� | |
���Գ��� | 6 | 24 | |
Ů�Գ��� | 2 | ||
�ܼ� | 30 |
��1��������Դ���ó�������![]() �������
�������![]() ���������ϵ��
���������ϵ��![]() �����ж�
�����ж�![]() ��
��![]() �Ƿ�������أ�
�Ƿ�������أ�
��2���뽫����![]() �������������������ж��Ƿ���
�������������������ж��Ƿ���![]() �İ�����Ϊ���������Ƿ�������Դ���ó����Ա��йأ�
�İ�����Ϊ���������Ƿ�������Դ���ó����Ա��йأ�
��3��������30�����������й�������Դ���ó��ij����Ա������Ϊ�õ�����������Դ���ó��ij����Ա����,�Ӹõ�����������Դ���ó��ij��������ѡȡ50��,��ѡ��Ů�Գ���������ΪX,��X����ѧ�����뷽��.
�ο���ʽ��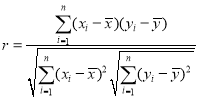 ��
��![]() ������
������![]() .
.![]() ����
����![]() ������ж�
������ж�![]() ��
��![]() �������.
�������.
������
| 0��10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��������![]() �ļ�ֵ��
�ļ�ֵ��
������ʵ��![]() Ϊ�������Ҷ������
Ϊ�������Ҷ������![]() ʱ������
ʱ������![]() ���������ʵ��
���������ʵ��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��.
��.
��1�����ۺ���![]() �ļ�ֵ��
�ļ�ֵ��
��2��������![]() ��
��![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ϵĺ���
�ϵĺ���![]() ��ͼ����һ���������ϵ����ߣ���������������
��ͼ����һ���������ϵ����ߣ���������������![]() �����dz�ֵ����.��
�����dz�ֵ����.��![]() �����зֵ�
�����зֵ�![]() ������
������![]() ���⻮�ֳ�
���⻮�ֳ�![]() ��С����
������![]() ����
����![]() ����Ϊ
����Ϊ![]() ��������
��������![]() ��
��![]() ���֡�����ܺ͡�.
���֡�����ܺ͡�.
��![]() ȡ�����ֵ��
ȡ�����ֵ��![]() ȡ����Сֵ
ȡ����Сֵ![]() ʱ����
ʱ����![]() ���ڡ���ѻ��֡�
���ڡ���ѻ��֡�![]() .
.
(1)��֪![]() ����
����![]() �����ֵ
�����ֵ![]() ��
��
(2)��֪![]() ����֤��
����֤��![]() ��
��![]() �ϴ��ڡ���ѻ��֡�
�ϴ��ڡ���ѻ��֡�![]() �ij�Ҫ������
�ij�Ҫ������![]() ��
��![]() �ϵ�������.
�ϵ�������.
(3)��![]() ��ż�����Ҵ��ڡ���ѻ��֡�
��ż�����Ҵ��ڡ���ѻ��֡�![]() ����֤��
����֤��![]() ��ż������
��ż������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ ����tΪ��������������ԭ��OΪ���㣬x���������Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ������2cos����2��5��4sin2����
����tΪ��������������ԭ��OΪ���㣬x���������Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ������2cos����2��5��4sin2����
��1����ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
��2����ֱ��l������C���У���m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com