
【题目】在高中学习过程中,同学们常这样说:“如果你的物理成绩好,那么你的数学学习就不会有什么大问题.”某班针对“高中物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系,如表为该班随机抽取6名学生在一次考试中的物理和数学成绩:
学生编号 学科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成绩(x) | 75 | 65 | 75 | 65 | 60 | 80 |
数学成绩(y) | 125 | 117 | 110 | 103 | 95 | 110 |
(1)求数学成绩y对物理成绩x的线性回归方程;
(2)该班某同学的物理成绩100分,预测他的数学成绩.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]()
参考数据:752+652+752+652+602+802=29700,
75×125+65×117+75×110+65×103+60×95+80×110=46425.
科目:高中数学 来源: 题型:
【题目】某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
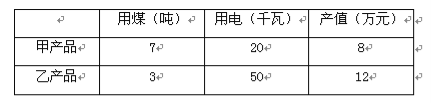
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 边的中点,现把
边的中点,现把![]() 沿
沿![]() 折叠,使其与
折叠,使其与![]() 构成如图2所示的三棱锥
构成如图2所示的三棱锥![]() ,且
,且![]() .
.
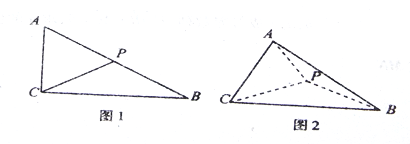
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 夹角的余弦值.
夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ﹣
﹣![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的点.
上的点.
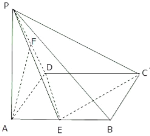
(1)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() ∥平面
∥平面![]() .
.
(2)当![]() :
:![]() = 2:1时,求二面角
= 2:1时,求二面角![]() ﹣
﹣![]() ﹣
﹣![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累积答对3题或打错3题即终止其初赛的比赛:答对3题者直接进入初赛,打错3题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为![]() .
.
(1)求选手甲可进入决赛的概率.
(2)设选手甲在初赛中答题的个数为![]() ,试求
,试求![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量, ![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
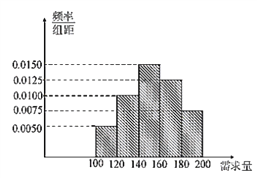
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数;
的平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4000元的概率.
不少于4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
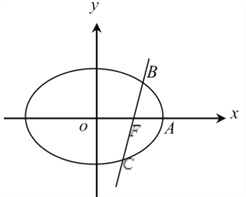
【题目】【2018届四川省成都市第七中学高三上学期模拟】已知椭圆![]() 的一个焦点
的一个焦点![]() ,且过点
,且过点![]() ,右顶点为
,右顶点为![]() ,经过点
,经过点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上一点,
上一点, ![]() 的角平分线交
的角平分线交![]() 轴于
轴于![]() ,求
,求![]() 的长;
的长;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得点
,使得点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 落在
落在![]() 上?若存在,求出
上?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸末,甲申、乙酉、丙戌…癸巳,…,共得到![]() 个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
A. 己亥年 B. 戊戌年 C. 辛丑年 D. 庚子年
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com