Question

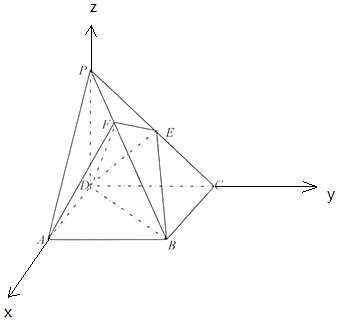
【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑． 如图，在阳马P﹣ABCD中，侧棱PD⊥底面ABCD，且PD=CD，E为PC中点，点F在PB上，且PB⊥平面DEF，连接BD，BE．
（Ⅰ）证明：DE⊥平面PBC；
（Ⅱ）试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；
（Ⅲ）已知AD=2， ，求二面角F﹣AD﹣B的余弦值．

Answer 1

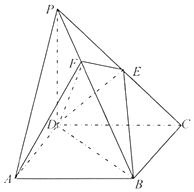
【答案】证明：（Ⅰ）因为PD⊥面ABCD，BC面ABCD，所以BC⊥PD．
因为四边形ABCD为矩形，
所以BC⊥DC．PD∩DC=D，
所以BC⊥面PDC．DE面PDC，DE⊥BC，
在△PDC中，PD=DC，E为PC中点，
所以DE⊥PC．又PC∩BC=C，
所以DE⊥面PBC．
解：（Ⅱ）四面体DBEF是鳖臑，
其中 ， ．
（Ⅲ）以DA，DC，DP所在直线为x轴，y轴，z轴建立空间直角坐标系．
则D（0，0，0），A（2，0，0）， ， ， ．
设 ，则 ．DF⊥PB得 ，解得 ．
所以 ．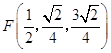
设平面FDA的法向量 ，
则 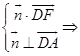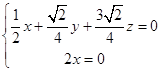，令z=1得x=0，y=﹣3．
平面FDA的法向量 ，
平面BDA的法向量 ，
， ．
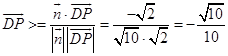二面角F﹣AD﹣B的余弦值为 ．

【解析】（Ⅰ）推导出BC⊥PD．BC⊥DC，从而BC⊥面PDC，进而DE⊥BC，再求出DE⊥PC，由此能证明DE⊥面PBC．（Ⅱ）四面体DBEF是鳖臑， ， ．（Ⅲ）以DA，DC，DP所在直线为x轴，y轴，z轴建立空间直角坐标系，利用向量法能求出二面角F﹣AD﹣B的余弦值．
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．