
【题目】若函数![]() 在
在![]() 上是单调函数,则a的取值范围是( )
上是单调函数,则a的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
由求导公式和法则求出f′(x),由条件和导数与函数单调性的关系分类讨论,分别列出不等式进行分离常数,再构造函数后,利用整体思想和二次函数的性质求出函数的最值,可得a的取值范围.
解:由题意得,f′(x)![]() ,
,
因为![]() 在[1,+∞)上是单调函数,
在[1,+∞)上是单调函数,
所以f′(x)≥0或f′(x)≤0在[1,+∞)上恒成立,
①当f′(x)≥0时,则![]() 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a![]() ,设g(x)
,设g(x)![]() ,
,
因为x∈[1,+∞),所以![]() ∈(0,1],
∈(0,1],
当![]() 1时,g(x)取到最大值是:0,
1时,g(x)取到最大值是:0,
所以a≥0,
②当f′(x)≤0时,则![]() 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a![]() ,设g(x)
,设g(x)![]() ,
,
因为x∈[1,+∞),所以![]() ∈(0,1],
∈(0,1],
当![]() 时,g(x)取到最大值是:
时,g(x)取到最大值是:![]() ,
,
所以a![]() ,
,
综上可得,a![]() 或a≥0,
或a≥0,
所以数a的取值范围是(﹣∞,![]() ]∪[0,+∞),
]∪[0,+∞),
故选:B.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在坐标轴上,且经过
的中心在原点,焦点在坐标轴上,且经过![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程和离心率;
(Ⅱ)四边形![]() 的四个顶点都在椭圆
的四个顶点都在椭圆![]() 上,且对角线
上,且对角线![]() ,
,![]() 过原点
过原点![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中,正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.若命题“![]() ”为真命题,则命题“
”为真命题,则命题“![]() ”为真命题
”为真命题
C.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D.“![]() ”是“命题‘
”是“命题‘![]() ’为真命题”的充分不必要条件
’为真命题”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校自主招生一次面试成绩的茎叶图和频率分布直方图均收到了不同程度的损坏,其可见部分信息如下,据此解答下列问题:
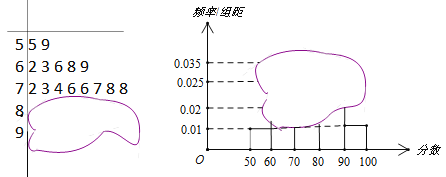
(1)求参加此次高校自主招生面试的总人数![]() 、面试成绩的中位数及分数在
、面试成绩的中位数及分数在![]() 内的人数;
内的人数;
(2)若从面试成绩在![]() 内的学生中任选三人进行随机复查,求恰好有二人分数在
内的学生中任选三人进行随机复查,求恰好有二人分数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com