
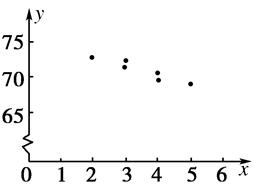
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量(千件) | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本(元/件) | 73 | 72 | 71 | 73 | 69 | 68 |

 ,
, )
)


科目:高中数学 来源:不详 题型:解答题
 的男生有30人,女生4人;身高<170的男生有10人。
的男生有30人,女生4人;身高<170的男生有10人。 列联表:
列联表:


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. =1.23x+4 =1.23x+4 | B. =1.23x+5 =1.23x+5 | C. =1.23x+0.08 =1.23x+0.08 | D. =0.08x+1.23 =0.08x+1.23 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 认为作业多 | 认为作业不多 | 总数 |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
 .
. | 0.050 | 0.025 | 0.010 | 0.001 |
 | 3.841 | 5.024 | 6.635 | 10.828 |
 的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”; 的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”; 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”; 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.身高一定是145.83 cm | B.身高在145.83 cm以上 |
| C.身高在145.83 cm左右 | D.身高在145.83 cm以下 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
,据此可以预测这个孩子10岁时的身高,则正确的叙述是( ) | A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月收入(单位百元) | [15,25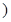 | [25,35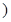 | [35,45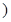 | [45,55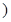 | [55,65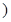 | [65,75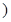 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 | 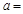 3 3 | 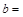 | |
| 不赞成 | 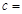 | 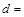 11 11 | |
| 合计 | | | 50 |
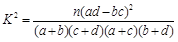 ,其中
,其中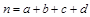 .)
.)P(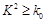 ) ) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
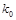 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.3 | C.2 | D.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com