
【题目】某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
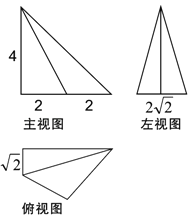
A. 136π B. 144π C. 36π D. 34π
【答案】D
【解析】分析:作出几何体的直观图,建立空间直角坐标系,求出外接球的球心,从而可的外接球的半径,再计算出外接球的面积.
详解:由三视图可知几何体为四棱锥E﹣ABCD,直观图如图所示:
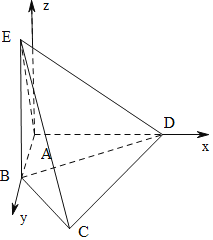
其中,BE⊥平面ABCD,BE=4,AB⊥AD,AB=![]() ,
,
C到AB的距离为2,C到AD的距离为2![]() ,
,
以A为原点,以AB,AD,及平面ABCD过A的垂线为坐标轴建立空间直角坐标系A﹣xyz,
则A(0,0,0),B(0,![]() ,0),C(2,2
,0),C(2,2![]() ,0),D(4,0,0),E(0,
,0),D(4,0,0),E(0,![]() ,4).
,4).
设外接球的球心为M(x,y,z),则MA=MB=MC=MD=ME,
∴x2+y2+z2=x2+(y﹣![]() )2+z2=(x﹣2)2+(y﹣2
)2+z2=(x﹣2)2+(y﹣2![]() )2+z2=(x﹣4)2+y2+z2=x2+(y﹣
)2+z2=(x﹣4)2+y2+z2=x2+(y﹣![]() )2+(z﹣4)2,
)2+(z﹣4)2,
解得x=2,y=![]() ,z=2.
,z=2.
∴外接球的半径r=MA=![]() =
=![]() ,
,
∴外接球的表面积S=4πr2=34π.
故选:D.


科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)=![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①等式f(-x)=-f(x)在x∈R时恒成立;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④方程f(x)=x在R上有三个根.
其中正确结论的序号有______.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益M、养鸡的收益N与投入a(单位:万元)满足 .设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作社的投入,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一、高二、高三的三个年级学生人数如下表
高三 | 高二 | 高一 | |
女生 | 100 | 150 | z |
男生 | 300 | 450 | 600 |
按年级分层抽样的方法评选优秀学生50人,其中高三有10人.
(1)求z的值;
(2)用分层抽样的方法在高一中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1名女生的概率;
(3)用随机抽样的方法从高二女生中抽取8人,经检测她们的得分如下:9.4,8.6,9.2, 9.6,8.7,9.3,9.0,8.2,把这8人的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往旅游,他先前进了![]() ,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了
,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了![]() , 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离
, 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离![]() 与时间
与时间![]() 的函数关系的图象大致为( )
的函数关系的图象大致为( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() (m,
(m,![]() ,m,n互质),下列关于
,m,n互质),下列关于![]() 的结论正确的是( )
的结论正确的是( )
A.m,n是奇数时,幂函数![]() 是奇函数
是奇函数
B.m是偶数,n是奇数时,幂函数![]() 是偶函数
是偶函数
C.m是奇数,n是偶数时,幂函数![]() 是偶函数
是偶函数
D.![]() 时,幂函数
时,幂函数![]() 在
在![]() 上是减函数
上是减函数
E.m,n是奇数时,幂函数![]() 的定义域为
的定义域为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.函数值域中的每一个数在定义域中一定只有一个数与之对应
B.函数的定义域和值域可以是空集
C.函数的定义域和值域一定是数集
D.函数的定义域和值域确定后,函数的对应关系也就确定了
E.函数的定义域和对应关系确定后,函数的值域也就确定了
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com