
【题目】一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8, 
(1)求频率分布直方图中a,b的值;
(2)根据频率分布直方图,估计这20棵果树产量的中位数;
(3)根据频率分布直方图,估计这1000棵果树的总产量.
【答案】
(1)解:由样本中产量在区间(45,50]上的果树棵数为8,
得a×5×20=8,解得a=0.08;
又因为5×(0.06+0.08+b+0.02)=1,
解得b=0.04,
所以a=0.08,b=0.04;
(2)解:设这20棵果树产量的中位数为x,
因为样本中产量在区间(40,45]上的频率为0.06×5=0.03,
样本中产量在区间(45,50]上的频率为0.08×5=0.4,
所以中位数在区间(45,50]内,
令0.06×5+(x﹣45)×0.08=0.5,
解得x=47.5,
所以估计这20棵果树产量的中位数为47.5;
(3)解:设这20棵果树产量的平均数是 ![]() ,
,
则 ![]() =5×(42.5×0.06+47.5×0.08+52.5×0.04+57.5×0.02)=48(kg);
=5×(42.5×0.06+47.5×0.08+52.5×0.04+57.5×0.02)=48(kg);
根据样本数据估计这1000棵果树的总产量为48×1000=48000(kg)
【解析】(1)由频率= ![]() ,利用频率和为1,即可求出a、b的值;(2)利用频率分布直方图中中位数两侧的频率相等,列出方程求出中位数x;(3)求出这20棵果树产量的平均数
,利用频率和为1,即可求出a、b的值;(2)利用频率分布直方图中中位数两侧的频率相等,列出方程求出中位数x;(3)求出这20棵果树产量的平均数 ![]() ,用样本数据估计总体的产量即可.
,用样本数据估计总体的产量即可.
【考点精析】通过灵活运用频率分布直方图,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 ![]() .
.
(1)求椭圆C的方程;
(2)已知动直线y=k(x+1)与椭圆C相交于A、B两点.
①若线段AB中点的横坐标为﹣ ![]() ,求斜率k的值;
,求斜率k的值;
②若点M(﹣ ![]() ,0),求证:
,0),求证: ![]()
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假
B.命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆”
C.命题“若k<9,则方程“ ![]() +
+ ![]() =1表示双曲线”是假命题
=1表示双曲线”是假命题
D.命题“在△ABC中,若sinA< ![]() ,则A<
,则A< ![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,AB=5,BC=4,AC=CC1=3,D为AB的中点 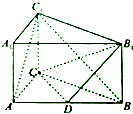
(1)求证:AC⊥BC1;
(2)求异面直线AC1与CB1所成角的余弦值;
(3)求二面角D﹣CB1﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,设
命题p:函数y=logax在区间(0,+∞)内单调递减;
q:曲线y=x2+(2a﹣3)x+1与x轴有两个不同的交点,
如果p∧q为真命题,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2 ![]() 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com