
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( ) 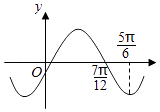
A.向左平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量 ![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗 ![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
参考公式: 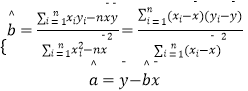
(1)已知产量 ![]() 和能耗
和能耗 ![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出 ![]() 关于
关于 ![]() 的线性回归方程
的线性回归方程 ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣ ![]() sinx
sinx ![]() cosx+1
cosx+1
(1)求函数f(x)的最小正周期和单调递增区间; (Ⅱ)若x∈[0, ![]() ],且f(x)=
],且f(x)= ![]() ,求cosx的值.
,求cosx的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一高中经过层层上报,被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队,队员来自高中三个年级,人数为50人.视力对踢足球有一定的影响,因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间,将测量结果按如下方式分成6组:第一组[4.75,4.85),第二组[4.85,4.95),…,第6组[5.25,5.35],如图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中,全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布N(5.01,0.0064). 参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,
P(μ﹣2σ<ξ≤μ+2σ)=0.9544,P(μ﹣3σ<ξ≤μ+3σ)=0.9974.
(1)试评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况; 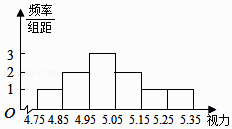
(2)求这50名队员视力在5.15以上(含5.15)的人数;
(3)在这50名队员视力在5.15以上(含5.15)的人中任意抽取2人,该2人中视力排名(从高到低)在全省喜爱足球的高中生中前130名的人数记为ξ,求ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为正整数集的函数f(x)= 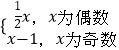 ,f1(x)=f(x),fn(x)=f[fn﹣1(x)].若fn(21)=1,则n=;若f4(x)=1,则x所有的值构成的集合为 .
,f1(x)=f(x),fn(x)=f[fn﹣1(x)].若fn(21)=1,则n=;若f4(x)=1,则x所有的值构成的集合为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需用A,B两种原料,已知每种产品各生产1吨所需原料及每天原料的可用限额如下表所示,如果生产1吨甲产品可获利润3万元,生产1吨乙产品可获利4万元,则该企业每天可获得最大利润为万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com