
(本小题满分12分)为了参加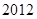 年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出
年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出 人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 | 高三(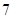 )班 )班 | 高三(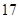 )班 )班 | 高二( )班 )班 | 高二(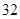 )班 )班 |
| 人数 |  | 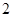 |  |  |
 名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为
名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为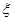 ,求随机变量
,求随机变量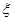 的分布列及数学期望
的分布列及数学期望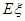 .
. 科目:高中数学 来源: 题型:解答题
为了参加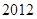 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 | 高三(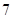 )班 )班 | 高三(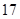 )班 )班 | 高二(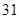 )班 )班 | 高二(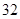 )班 )班 |
| 人数 | 12 | 6 | 9 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题14分)口袋内有 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和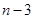 个白球.已知从
个白球.已知从
口袋中随机取出一个球是红球的概率是 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。
(Ⅰ)求 和
和 ;
;
(Ⅱ)不放回地从口袋中取球(每次只取一个球),取到白球时即停止取球,记 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 的分布列和期望
的分布列和期望 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题10分)某校高三某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求分数在[50,60)的频率及全班人数;(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求分数在[90,100]之间的份数 的数学期望
的数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
公安部发布酒后驾驶处罚的新规定(一次性扣罚12分)已于2011年4月1日起正式施行.酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量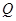 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当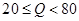 时,为酒后驾车;当
时,为酒后驾车;当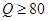 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
依据上述材料回答下列问题:
(Ⅰ)分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率;
(Ⅱ)从酒后违法驾车的司机中,抽取2人,请一一列举出所有的抽取结果,并求取到的2人中含有醉酒驾车的概率. (酒后驾车的人用大写字母如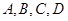 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如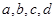 表示)
表示)
| 血酒含量 | (0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
| 人数 | 194 | 1 | 2 | 1 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分 )袋中有大小相同的红、黄两种颜色的球各1个,从中任取1只,有放回地抽取3次.求:
(1)3只全是红球的概率;
(2)3只颜色全相同的概率;
(3)3只颜色不全相同的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知关于x的二次函数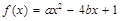 .
.
(I)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数 在区间
在区间 上是增函数的概率;
上是增函数的概率;
(II)设点(a,b)是区域 内的一点,求函数
内的一点,求函数 在区间
在区间 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为 ,求E
,求E .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com