
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数, ![]()
(I)若![]() ,函数
,函数![]()
①求函数![]() 的单调区间
的单调区间
②若函数 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围
的取值范围
(II)若存在实数![]() ,使得
,使得![]() ,且
,且![]() ,求证:
,求证: ![]()
【答案】(1)①详见解析②实数![]() 的取值范围是
的取值范围是![]() ;(2)
;(2)![]() ;
;
【解析】试题分析:(1)①求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
②求出函数的导数,通过讨论m的范围得到函数的值域,从而确定m的具体范围即可;
(2)求出函数f(x)的导数,得到a>0且f(x)在(﹣∞,![]() ]递减,在[
]递减,在[![]() ,+∞)递增,设
,+∞)递增,设![]() ,则有
,则有![]() ,根据函数的单调性得到关于m的不等式组,解出即可.
,根据函数的单调性得到关于m的不等式组,解出即可.
试题解析:
(1)当![]() 时,
时, ![]() .
.
①![]() .
.
由![]() 得
得![]() ,由
,由![]() 得
得![]() .
.
所以函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
②![]()
当![]() 时,
时, ![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增.
上单调递增.
![]() 在
在![]() 上单调递减,值域为
上单调递减,值域为![]() ,
,
因为![]() 的值域为
的值域为![]() ,所以
,所以![]() ,
,
即![]() .
. ![]()
由①可知当![]() 时,
时, ![]() ,故
,故![]() 不成立.
不成立.
因为![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且![]()
所以当![]() 时,
时, ![]() 恒成立,因此
恒成立,因此![]() .
.
![]() 当
当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 上的值域为
上的值域为![]() ,即
,即![]() .
.
![]() 在
在![]() 上单调递减,值域为
上单调递减,值域为![]() .
.
因为![]() 的值域为
的值域为![]() ,所以
,所以![]() ,即
,即![]() .
.
综合1°,2°可知,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() .
.
若![]() 时,
时, ![]() ,此时
,此时![]() 在
在![]() 上单调递增.
上单调递增.
由![]() 可得
可得![]() ,与
,与![]() 相矛盾,
相矛盾,
同样不能有![]() .
.
不妨设![]() ,则有
,则有![]() .
.
因为![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
所以当![]() 时,
时, ![]() .
.
由![]() ,且
,且![]() ,可得
,可得![]()
故![]() .
.
又![]() 在
在![]() 单调递减,且
单调递减,且![]() ,所以
,所以![]() ,
,
所以![]() ,同理
,同理![]() .
.
即![]() 解得
解得![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() :
: ![]() 上,而
上,而![]() 为
为![]() 在
在![]() 轴上的投影,且点
轴上的投影,且点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上两点,且
上两点,且![]() ,
, ![]() 为坐标原点,求
为坐标原点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )

①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 .
.
(1)写出直线![]() 与曲线
与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点M平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南京市江北新区计划在一个竖直长度为20米的瀑布![]() 正前方修建一座观光电梯
正前方修建一座观光电梯![]() 。如图所示,瀑布底部
。如图所示,瀑布底部![]() 距离水平地面的高度
距离水平地面的高度![]() 为60米,电梯上设有一个安全拍照口
为60米,电梯上设有一个安全拍照口![]() ,
, ![]() 上升的最大高度为60米。设
上升的最大高度为60米。设![]() 距离水平地面的高度为
距离水平地面的高度为![]() 米,
米, ![]() 处拍照瀑布的视角
处拍照瀑布的视角![]() 为
为![]() 。摄影爱好者发现,要使照片清晰,视角
。摄影爱好者发现,要使照片清晰,视角![]() 不能小于
不能小于![]() 。
。
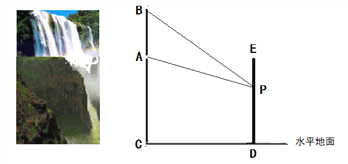
(1)当![]() 米时,视角
米时,视角![]() 恰好为
恰好为![]() ,求电梯和山脚的水平距离
,求电梯和山脚的水平距离![]() 。
。
(2)要使电梯拍照口![]() 的高度
的高度![]() 在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离
在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com