
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求证:当![]() 时,
时,![]() ;
;
(Ⅲ)设实数k使得![]() 对
对![]() 恒成立,求k的最大值.
恒成立,求k的最大值.
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 5 | -5 | 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解析式;
的解析式;
(Ⅱ)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]() 个单位长度,得到
个单位长度,得到![]() 的图象. 若
的图象. 若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的回归方程![]()
(2)用所求回归方程预测该地区2015年(![]() )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程![]() 中
中
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为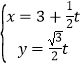 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已成椭圆 ![]() 的左右顶点分别为
的左右顶点分别为 ![]() ,上下顶点分别为
,上下顶点分别为 ![]() ,左右焦点分别为
,左右焦点分别为 ![]() ,其中长轴长为4,且圆
,其中长轴长为4,且圆 ![]() 为菱形
为菱形 ![]() 的内切圆.
的内切圆.
(1)求椭圆 ![]() 的方程;
的方程;
(2)点 ![]() 为
为 ![]() 轴正半轴上一点,过点
轴正半轴上一点,过点 ![]() 作椭圆
作椭圆 ![]() 的切线
的切线 ![]() ,记右焦点
,记右焦点 ![]() 在
在 ![]() 上的射影为
上的射影为 ![]() ,若
,若 ![]() 的面积不小于
的面积不小于 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个集合A,B,满足BA.若对任意的x∈A,存在ai , aj∈B(i≠j),使得x=λ1ai+λ2aj(λ1 , λ2∈{﹣1,0,1}),则称B为A的一个基集.若A={1,2,3,4,5,6,7,8,9,10},则其基集B元素个数的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com