
【题目】已知函数f(x)=x3﹣ax,g(x)= ![]() x2﹣lnx﹣
x2﹣lnx﹣ ![]() .
.
(1)若f(x)和g(x)在同一点处有相同的极值,求实数a的值;
(2)对于一切x∈(0,+∞),有不等式f(x)≥2xg(x)﹣x2+5x﹣3恒成立,求实数a的取值范围;
(3)设G(x)= ![]() x2﹣
x2﹣ ![]() ﹣g(x),求证:G(x)>
﹣g(x),求证:G(x)> ![]() ﹣
﹣ ![]() .
.
【答案】
(1)解:∵g′(x)=x﹣ ![]() =
= ![]() ,∴当x∈(0,1)时,g'(x)<0,则g(x)单调递减;当x∈(1,+∞)时,g'(x)>0,则g(x)单调递增.∴g(x)极小值=g(1)=﹣2
,∴当x∈(0,1)时,g'(x)<0,则g(x)单调递减;当x∈(1,+∞)时,g'(x)>0,则g(x)单调递增.∴g(x)极小值=g(1)=﹣2
又∵f(x)和g(x)在同一点处有相同的极值,
∴f(1)=1﹣a=﹣2,即a=3
(2)解:若使对于一切x∈(0,+∞),不等式f(x)≥2xg(x)﹣x2+5x﹣3恒成立,则只需使得不等式 ![]() 恒成立,即只需
恒成立,即只需 ![]()
设 ![]() ,则
,则 ![]() ,
,
∴当x∈(0,1)时,t'(x)<0,则t(x)单调递减;当x∈(1,+∞)时,t'(x)>0,则t(x)单调递增.
∴t(x)最小值=t(1)=4,
∴a≤4,即a的取值范围为(﹣∞,4]
(3)解:若证 ![]() ,则只需证明
,则只需证明 ![]() ,即证
,即证 ![]()
设m(x)=xlnx,则m'(x)=lnx+1,由于m(x)在 ![]() 单调递减,在
单调递减,在 ![]() 单调递增,所以
单调递增,所以 ![]() ;设
;设 ![]() ,则
,则 ![]() ,由于n(x)在(0,1)单调递增,在(1,+∞)单调递减,所以
,由于n(x)在(0,1)单调递增,在(1,+∞)单调递减,所以 ![]() .
.
所以m(x)≥n(x)又由于m(x)与n(x)不在同一个变量时取得最值,即m(x)>n(x)
综上所述, ![]()
【解析】(1)求出函数的导数,判断导函数的符号,求出函数的极小值,然后列出方程求解a 即可.(2)使对于一切x∈(0,+∞),不等式f(x)≥2xg(x)﹣x2+5x﹣3恒成立,转化为 ![]() 恒成立,只需
恒成立,只需 ![]() ,构造函数,利用函数的导数求解函数的最小值,推出a的范围即可.(3)若证
,构造函数,利用函数的导数求解函数的最小值,推出a的范围即可.(3)若证 ![]() ,则只需证明
,则只需证明 ![]() ,即证
,即证 ![]() ,构造函数设m(x)=xlnx,利用函数的单调性求解函数的极值,推出结果即可.
,构造函数设m(x)=xlnx,利用函数的单调性求解函数的极值,推出结果即可.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(ωx+φ)(ω>0,﹣
sin(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() ),A(
),A( ![]() ,0)为f(x)图象的对称中心,B,C是该图象上相邻的最高点和最低点,若BC=4,则f(x)的单调递增区间是( )
,0)为f(x)图象的对称中心,B,C是该图象上相邻的最高点和最低点,若BC=4,则f(x)的单调递增区间是( )
A.(2k﹣ ![]() ,2k+
,2k+ ![]() ),k∈Z
),k∈Z
B.(2kπ﹣ ![]() π,2kπ+
π,2kπ+ ![]() π),k∈Z
π),k∈Z
C.(4k﹣ ![]() ,4k+
,4k+ ![]() ),k∈Z
),k∈Z
D.(4kπ﹣ ![]() π,4kπ+
π,4kπ+ ![]() π),k∈Z
π),k∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=eax(a≠0).
(1)当 ![]() 时,令
时,令 ![]() (x>0),求函数g(x)在[m,m+1](m>0)上的最小值;
(x>0),求函数g(x)在[m,m+1](m>0)上的最小值;
(2)若对于一切x∈R,f(x)﹣x﹣1≥0恒成立,求a的取值集合;
(3)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为 ![]() .
.
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为ξ,求ξ的分布列,数学期望以及方差;大气污染会引起各种疾病,试浅谈日常生活中如何减少大气污染.
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式K2= ![]() 其中n=a+b+c+d)
其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x﹣2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex﹣ ![]() ,a=f(﹣5),b=f(
,a=f(﹣5),b=f( ![]() ).c=f(
).c=f( ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a<b<c
B.c<a<b
C.c<a<b
D.b<a<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a和b是任意非零实数.
(1)求 ![]() 的最小值.
的最小值.
(2)若不等式|2a+b|+|2a﹣b|≥|a|(|2+x|+|2﹣x|)恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1 , AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1 , DF交于点E,且AB1⊥DF,则下列结论中不正确的是( ) 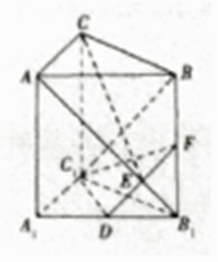
A.CE与BC1异面且垂直
B.AB1⊥C1F
C.△C1DF是直角三角形
D.DF的长为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com