
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.
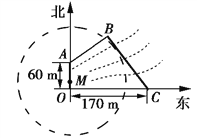
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
【答案】(1) 150 m (2) |OM|=10 m
【解析】试题分析:本题是应用题,我们可用解析法来解决,为此以![]() 为原点,以向东,向北为坐标轴建立直角坐标系.(1)
为原点,以向东,向北为坐标轴建立直角坐标系.(1)![]() 点坐标炎
点坐标炎![]() ,
, ![]() ,因此要求
,因此要求![]() 的长,就要求得
的长,就要求得![]() 点坐标,已知
点坐标,已知![]() 说明直线
说明直线![]() 斜率为
斜率为![]() ,这样直线
,这样直线![]() 方程可立即写出,又
方程可立即写出,又![]() ,故
,故![]() 斜率也能得出,这样
斜率也能得出,这样![]() 方程已知,两条直线的交点
方程已知,两条直线的交点![]() 的坐标随之而得;(2)实质就是圆半径最大,即线段
的坐标随之而得;(2)实质就是圆半径最大,即线段![]() 上哪个点到直线
上哪个点到直线![]() 的距离最大,为此设
的距离最大,为此设![]() ,由
,由![]() ,圆半径
,圆半径![]() 是圆心
是圆心![]() 到直线
到直线![]() 的距离,而求它的最大值,要考虑条件古桥两端
的距离,而求它的最大值,要考虑条件古桥两端![]() 和
和![]() 到该圆上任一点的距离均不少于80
到该圆上任一点的距离均不少于80![]() ,列出不等式组,可求得
,列出不等式组,可求得![]() 的范围,进而求得最大值.当然本题如果用解三角形的知识也可以解决.
的范围,进而求得最大值.当然本题如果用解三角形的知识也可以解决.
试题解析:

(1)如图,以![]() 为
为![]() 轴建立直角坐标系,则
轴建立直角坐标系,则![]() ,
, ![]() ,由题意
,由题意![]() ,直线
,直线![]() 方程为
方程为![]() .又
.又![]() ,故直线
,故直线![]() 方程为
方程为![]() ,由
,由 ,解得
,解得![]() ,即
,即![]() ,所以
,所以![]()
![]() ;
;
(2)设![]() ,即
,即![]()
![]() ,由(1)直线
,由(1)直线![]() 的一般方程为
的一般方程为![]() ,圆
,圆![]() 的半径为
的半径为![]() ,由题意要求
,由题意要求![]() ,由于
,由于![]() ,因此
,因此![]()
![]() ,∴
,∴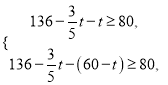 ∴
∴![]() ,所以当
,所以当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,此时圆面积最大.
,此时圆面积最大.


科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为 ![]() ,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
(1)求椭圆E的方程;
(2)求l1的斜率k的取值范围;
(3)求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商场购物,且参加者必须从淘宝和京东商城选择一家购物.
(1)求这4人中恰有1人去淘宝网购物的概率;
(2)用ξ、η分别表示这4人中去淘宝网和京东商城购物的人数,记X=ξη,求随机变量X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=![]() ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;
(2)若圆C1与圆C2相内切,求圆C2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |
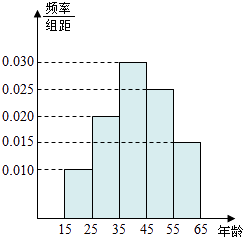
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P的切线方程;
(2)若f(x)≤0恒成立求m的取值范围;
(3)求函数f(x)在区间[1,e]上最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.

(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( ) 
A.210﹣1
B.210
C.310﹣1
D.310
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com