
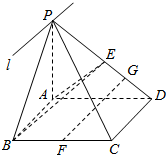
 如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.
如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.分析 (1)证明AB∥面PCD,然后证明l∥AB.
(2)(文)取PA中点M,连接BM,EM,证明四边形BFEM为平行四边形,然后利用直线与平面平行的判定定理证明EF∥面PAB.
(3)(理)取AD中点N,证明FN∥面ABE,证明面FNG∥面ABE,说明G为ED中点,通过线段关系求出$\frac{PG}{GD}=3$.
解答 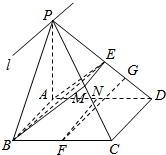 (1)证明:∵ABCD为平行四边形,∴AB∥CD,又AB?面PCD,
(1)证明:∵ABCD为平行四边形,∴AB∥CD,又AB?面PCD,
∴AB∥面PCD,∵面PAB∩面PCD=l,∴l∥AB.(6分)
(文)(2)取PC中点M,连接BM,EM,则$EM\underline{\underline{∥}}\frac{1}{2}AD$,又∵$BF\underline{\underline{∥}}\frac{1}{2}AD$,
∴$EM\underline{\underline{∥}}BF$,∴四边形BFEM为平行四边形,∴EF∥BM,
∵EF?面PAB,BM⊆面PAB,∴EF∥面PAB.(12分)
(理)(3)取AD中点N,则FN∥AB,∴FN∥面ABE,
∵FG∥面ABE,∴面FNG∥面ABE,
∴AE∥NG,又∵N为ED中点,∴G为ED中点,
∴EG=GD,又PE=ED,∴$\frac{PG}{GD}=3$. (12分)
点评 本题考查直线与平面平行,点线面距离的计算,考查空间想象能力以及逻辑推理能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{15}$ | C. | $3\sqrt{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
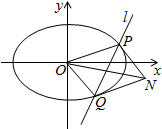 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.
如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,$\frac{\sqrt{6}}{2}$] | C. | [$\frac{\sqrt{6}}{2}$,+∞) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com