
分析 设D(x,y).由|CD|=1,可得$\sqrt{(x-3)^{2}+{y}^{2}}$=1,化为(x-3)2+y2=1.令$\left\{\begin{array}{l}{x=3+cosθ}\\{y=sinθ}\end{array}\right.$(θ∈[0,2π)).$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$=(1+x,3+y).利用模的计算公式可得|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|,再利用三角函数的单调性即可得出.
解答 解:设D(x,y).
∵|CD|=1,∴$\sqrt{(x-3)^{2}+{y}^{2}}$=1,化为(x-3)2+y2=1.
令$\left\{\begin{array}{l}{x=3+cosθ}\\{y=sinθ}\end{array}\right.$(θ∈[0,2π)).
∴$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$=(1+x,3+y).
∴|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|=$\sqrt{(1+x)^{2}+(3+y)^{2}}$=$\sqrt{(4+cosθ)^{2}+(3+sinθ)^{2}}$=$\sqrt{6sinθ+8cosθ+26}$=$\sqrt{10sin(θ+β)+26}$$≥\sqrt{26-10}$=4,当sin(θ+β)=-1时取等号.
∴|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|的最小值是4.
故答案为:4.
点评 本题考查了数量积的坐标运算性质、向量的坐标运算、圆的参数方程、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-2sinx | B. | f(x)=2sinx | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin2x+cos2x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{29}$ | C. | $3\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
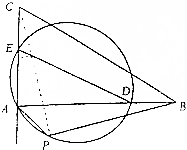 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com