
【题目】已知函数f(x)=ax2-(a+2)x+lnx
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对任意x1,x2∈(0,+∞),x1<x2,有f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.
【答案】(1) y=-2.
(2) [0,8].
【解析】分析:(1)求出导函数![]() ,可得切线斜率
,可得切线斜率![]() ,切线方程为
,切线方程为![]() ,化简即可;
,化简即可;
(2)若对任意x1,x2∈(0,+∞),x1<x2,有f(x1)+2x1<f(x2)+2x2恒成立,说明函数![]() 是
是![]() 上的增函数,从而
上的增函数,从而![]() 在
在![]() 上恒成立,再利用二次函数的性质可得
上恒成立,再利用二次函数的性质可得![]() 的范围.
的范围.
详解: (1)a=1时,f(x)=x2-3x+lnx,f(1)=-2,∴f ′(x)=2x-3+![]() ,
,
∴曲线y=f(x)在点(1,f(1))处的切线斜率k=f ′(1)=0;
所以在点(1,f(1))处的切线方程为 y=-2;
(2)令g(x)=f(x)+2x=ax2-ax+lnx,(x>0);由题意知g(x)在(0,+∞)单调递增,所以g′(x)=2ax-a+![]() ≥0在(0,+∞)上恒成立,即2ax2-ax+1≥0在(0,+∞)上恒成立;令h(x)=2ax2-ax+1,(x>0);
≥0在(0,+∞)上恒成立,即2ax2-ax+1≥0在(0,+∞)上恒成立;令h(x)=2ax2-ax+1,(x>0);
则①若a=0,h(x)=1≥0恒成立;
②若a<0,二次函数h(x)≥0不恒成立,舍去;
③若a>0,二次函数h(x)≥0恒成立,只需满足最小值h(![]() )≥0,即
)≥0,即![]() -
-![]() +1≥0,解得0<a≤8;
+1≥0,解得0<a≤8;
综上,a的取值范围是[0,8].


科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | A |
|
|
女 |
|
|
|
合计 |
| B |
|
(1)根据已知条件求出上面的![]() 列联表中的A和B;用分层抽样的方法在患心肺疾病的人群中抽
列联表中的A和B;用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,并说明是否有
,并说明是否有![]() 的把握认为心肺疾病与性别有关?
的把握认为心肺疾病与性别有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: ![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线方程为
的准线方程为![]() ,点
,点![]() 为坐标原点,不过点
为坐标原点,不过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() .
.
(1)如果直线![]() 过点
过点![]() ,求证:
,求证:![]() ;
;
(2)如果![]() ,证明:直线
,证明:直线![]() 必过一定点,并求出该定点.
必过一定点,并求出该定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|x|+a.
(1)若a=0,求不等式f(x)≥x的解集;
(2)若对任意x∈R,f(x)≥0恒成立,求a的范围;
(3)若方程f(x)=x有三个不同的解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1)
附:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
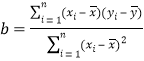 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() ,其中
,其中 ![]() .
.
(1)试讨论函数 ![]() 的单调性;
的单调性;
(2)已知当 ![]() (其中
(其中 ![]() 是自然对数的底数)时,在
是自然对数的底数)时,在 ![]() 上至少存在一点
上至少存在一点 ![]() ,使
,使 ![]() 成立,求
成立,求 ![]() 的取值范围;
的取值范围;
(3)求证:当 ![]() 时,对任意
时,对任意 ![]() ,
,![]() ,有
,有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业招聘大学毕业生,经过综合测试,录用了14名女生和6名男生,这20名学生的测试成绩如茎叶图所示(单位:分),记成绩不小于80分者为![]() 等,小于80分者为
等,小于80分者为![]() 等.
等.

(1)求女生成绩的中位数及男生成绩的平均数;
(2)如果用分层抽样的方法从![]() 等和
等和![]() 等中共抽取5人组成“创新团队”,则从
等中共抽取5人组成“创新团队”,则从![]() 等和
等和![]() 等中分别抽几人?
等中分别抽几人?
(3)在(2)问的基础上,现从该“创新团队”中随机抽取2人,求至少有1人是![]() 等的概率.
等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com