解:(1)由题意 1+a
1+a
2+…+a
n-λa
n+1=0①
1+a
1+a
2+…+a
n+a
n+1-λa
n+2=0②
由②-①得(1+λ)a
n+1-λa
n+2=0,又λ≠0,λ≠-1,n∈N
*,
∴
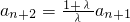
,
故数列{a
n}从第二项开始为等比数列…(3分)
将n=1代入①式,
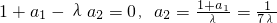
∴n≥2时,
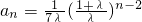
∴数列{a
n}的通项
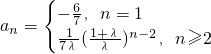
…(6分)
(2)∵
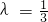
,
∴
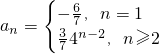
∵假设存在任意三项a
m,a
k,a
p成等差数列
①不妨设当m>k>p≥2,
∵当n≥2时,数列{a
n}单调递增,
∴2a
k=a
m+a
p,
∴
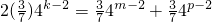
,
∴2•4
k-p=4
m-p+1,
由上式知:左边=偶数≠右边=奇数,
∴当n≥2时,数列{a
n}不存在三项成等差数列.…(9分)
②假设存在成等差数列的三项中包含a
1时
不妨设m=1,k>p≥2且a
k>a
p,
∵当n≥2时,a
n>a
1,
∴2a
p=a
1+a
k,
∴

,
∴2•4
p-2=-2+4
k-2,
∴2
(2p-3)=2
2(k-2)-2,
∵k>p≥2,
∴当且仅当k=3,p=2时成立,
∴数列{a
n}存在a
1,a
2,a
3或a
3,a
2,a
1成等差数列.…(12分)
分析:(1)由题意 1+a
1+a
2+…+a
n-λa
n+1=0,则1+a
1+a
2+…+a
n+a
n+1-λa
n+2=0,故(1+λ)a
n+1-λa
n+2=0,又λ≠0,λ≠-1,n∈N
*,所以
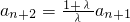
,由此能求出数列{a
n}的通项公式.
(2)由
,知
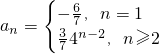
,假设存在任意三项a
m,a
k,a
p成等差数列.由此入手能够导出数列{a
n}存在a
1,a
2,a
3或a
3,a
2,a
1成等差数列.
点评:本题考查数列的通项公式的求法,探索数列{a
n}中是否存在三项成等差数列.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答,注意培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

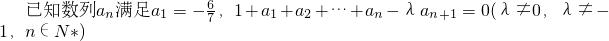 .
. 时,数列{an}中是否存在三项成等差数列,若存在,请求出来;若不存在,请说明理由.
时,数列{an}中是否存在三项成等差数列,若存在,请求出来;若不存在,请说明理由.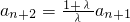 ,
,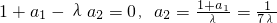
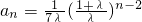
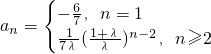 …(6分)
…(6分)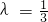 ,
,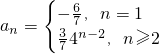
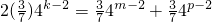 ,
, ,
,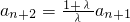 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.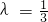 ,知
,知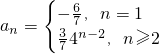 ,假设存在任意三项am,ak,ap成等差数列.由此入手能够导出数列{an}存在a1,a2,a3或a3,a2,a1成等差数列.
,假设存在任意三项am,ak,ap成等差数列.由此入手能够导出数列{an}存在a1,a2,a3或a3,a2,a1成等差数列.
