
【题目】某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是![]() .
.

(1)若成绩在![]() 的学生中男生比女生多一人,从成绩在
的学生中男生比女生多一人,从成绩在![]() 的学生中任选2人,求此2人都是男生的概率;
的学生中任选2人,求此2人都是男生的概率;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,已知第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )

A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ;第二组
;第二组![]() ;…;第八组
;…;第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.

(1)估计这所学校高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为![]() ,求满足“
,求满足“![]() ”的事件的概率.
”的事件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( ) 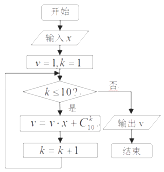
A.210﹣1
B.210
C.310﹣1
D.310
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的通项公式为
的通项公式为![]() (
(![]() ,
, ![]() ),数列
),数列![]() 定义如下:对于正整数
定义如下:对于正整数![]() ,
, ![]() 是使得不等式
是使得不等式![]() 成立的所有
成立的所有![]() 中的最小值.
中的最小值.
(1)若![]() ,
, ![]() ,求
,求![]() ;
;
(2)若![]() ,
, ![]() ,求数列
,求数列![]() 的前
的前![]() 项和公式;
项和公式;
(3)是否存在![]() 和
和![]() ,使得
,使得![]()
![]() ?如果存在,求
?如果存在,求![]() 和
和![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com