
【题目】设有二元关系![]() ,已知曲线
,已知曲线![]() .
.
(1)若![]() 时,正方形
时,正方形![]() 的四个顶点均在曲线
的四个顶点均在曲线![]() 上,求正方形
上,求正方形![]() 的面积;
的面积;
(2)设曲线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,抛物线
,抛物线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,求证直线
,求证直线![]() 过定点,并求该定点的坐标;
过定点,并求该定点的坐标;
(3)设曲线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,
,![]() ,可知动点
,可知动点![]() 在某确定的曲线
在某确定的曲线![]() 上运动,曲线
上运动,曲线![]() 上与上述曲线
上与上述曲线![]() 在
在![]() 时共有4个交点,其坐标分别是
时共有4个交点,其坐标分别是![]() 、
、![]() 、
、![]() 、
、![]() ,集合
,集合![]() 的所有非空子集设为
的所有非空子集设为![]() ,将
,将![]() 中的所有元素相加(若
中的所有元素相加(若![]() 只有一个元素,则和是其自身)得到255个数
只有一个元素,则和是其自身)得到255个数![]() ,求所有正整数
,求所有正整数![]() 的值,使得
的值,使得![]() 是一个与变数
是一个与变数![]() 及变数
及变数![]() 均无关的常数.
均无关的常数.
【答案】(1)4;(2)直线![]() 过定点
过定点![]() ;(3)
;(3)![]() 是奇数时,
是奇数时,![]() 是一个与变数
是一个与变数![]() 及变数
及变数![]() 均无关的常数.
均无关的常数.
【解析】
(1)令![]() ,解得
,解得![]() ,即
,即![]() 表示两条平行直线,这两条平行线间的距离2为正方形的边长,由此可得正方形面积;
表示两条平行直线,这两条平行线间的距离2为正方形的边长,由此可得正方形面积;
(2)曲线![]() 中,令
中,令![]() ,则
,则![]() ,设
,设![]() ,由韦达定理得
,由韦达定理得![]() ,写出
,写出![]() 的方程求得
的方程求得![]() 的坐标,从而得直线
的坐标,从而得直线![]() 的方程(只含有参数
的方程(只含有参数![]() ),观察方程可得直线
),观察方程可得直线![]() 所过定点;
所过定点;
(3)令![]() ,则
,则![]() ,则
,则![]() ,即点
,即点![]() 在曲线
在曲线![]() 上,而曲线
上,而曲线![]() 表示两条平行线且斜率为1,因此可知点
表示两条平行线且斜率为1,因此可知点![]() 关于直线
关于直线![]() 对称,从而可得
对称,从而可得![]() ,同理
,同理![]() .于是有
.于是有![]() ,有
,有![]() ,则
,则![]() 时,
时,![]() ,对其他244个子集配对:
,对其他244个子集配对:![]() ,满足
,满足![]() ,
,![]() ,这样的集合“对”共有127对。
,这样的集合“对”共有127对。
以下证明:对![]() 的元素和
的元素和![]() 和
和![]() 的元素和
的元素和![]() ,当
,当![]() 为奇数时,恒有
为奇数时,恒有![]() ,为此可用数学归纳法证明
,为此可用数学归纳法证明![]() 能够整除
能够整除![]() ,从而得结论.
,从而得结论.
(1)令![]() ,得
,得![]() ,即
,即![]() 表示两条平行直线,这两条平行线间的距离为
表示两条平行直线,这两条平行线间的距离为 ,此为正方形的边长,正方形的面积为4。
,此为正方形的边长,正方形的面积为4。
(2)在曲线![]() 中,令
中,令![]() ,则
,则![]() ,设
,设![]() ,由韦达定理得
,由韦达定理得![]() ,由题意知
,由题意知![]() ,直线
,直线![]() 方程为
方程为![]() ,
,![]() 方程为
方程为![]() ,
,

由 ,解得
,解得![]() ,同理可得
,同理可得![]() ,∵
,∵![]() ,∴
,∴![]() ,∴直线
,∴直线![]() 方程为
方程为![]() ,化简为:
,化简为:![]() ,
,![]() 时,
时,![]() ,故直线
,故直线![]() 过定点
过定点![]() ;
;
(3)令![]() ,则
,则![]() ,则
,则![]() ,即点
,即点![]() 在曲线
在曲线![]() 上,又曲线
上,又曲线![]() :
:![]() 恒表示两条平行直线
恒表示两条平行直线![]() ,如图,
,如图,
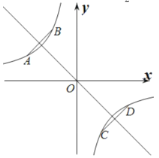
![]() 关于直线
关于直线![]() 对称,则
对称,则![]() ,即
,即![]() ,同理
,同理![]() ,则
,则![]() ,集合
,集合![]() 的所有非空子集设为
的所有非空子集设为![]() ,取
,取![]() ,显然
,显然![]() ,则
,则![]() 时,
时,![]() ,对
,对![]() 的其他子集,我们把它们配成集合“对”
的其他子集,我们把它们配成集合“对”![]() ,使得
,使得![]() ,
,![]() ,这样的集合“对”共有127对。
,这样的集合“对”共有127对。
以下证明:对![]() 的元素和
的元素和![]() 和
和![]() 的元素和
的元素和![]() ,当
,当![]() 为奇数时,恒有
为奇数时,恒有![]() ,为此先证明:
,为此先证明:![]() 是奇数时,则
是奇数时,则![]() 能够整除
能够整除![]() ,
,
用数学归纳法证之:
(i)当![]() 时显然成立,
时显然成立,
(ii)假设![]() (
(![]() 是奇数)成立,即
是奇数)成立,即![]() 能够整除
能够整除![]() ,则当
,则当![]() 时,
时,![]() ,
,
由归纳假设知此式能被![]() 整除,
整除,
由(i)(ii)可知当![]() 为奇数时,
为奇数时,![]() 能够整除
能够整除![]() .
.
∴![]() 为奇数时,
为奇数时,![]() (其中
(其中![]() 是关于
是关于![]() 的整式),
的整式),
∵![]() ,
,![]() ,∴对每一个集合“对”
,∴对每一个集合“对”![]() ,
,![]() ,
,
则一定有![]() =0,
=0,![]() ,于是
,于是![]() 是常数.
是常数.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线Γ的准线方程为![]() .焦点为
.焦点为![]() .
.
(1)求证:抛物线Γ上任意一点![]() 的坐标
的坐标![]() 都满足方程:
都满足方程:![]()
(2)请求出抛物线Γ的对称性和范围,并运用以上方程证明你的结论;
(3)设垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点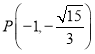 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,使得
两点,使得![]() ?若存在,求出直线的方程;若不存在,说明理由.
?若存在,求出直线的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(ax+b)﹣x(a,b∈R,ab≠0).
(1)讨论f(x)的单调性;
(2)若f(x)≤0恒成立,求ea(b﹣1)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com