
【题目】已知椭圆![]() 的焦距和长半轴长都为2.过椭圆
的焦距和长半轴长都为2.过椭圆![]() 的右焦点
的右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 的左顶点,直线
的左顶点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .求证:以
.求证:以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .以原点为极点,
.以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为C、D,且过点
的左、右顶点分别为C、D,且过点![]() ,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为
,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)O为坐标原点,设直线CP交定直线x = m于点M,当m为何值时,![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
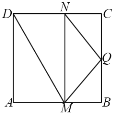
【题目】如图,在边长等于2正方形![]() 中,点Q是
中,点Q是![]() 中点,点M,N分别在线段
中点,点M,N分别在线段![]() 上移动(M不与A,B重合,N不与C,D重合),且
上移动(M不与A,B重合,N不与C,D重合),且![]() ,沿着
,沿着![]() 将四边形
将四边形![]() 折起,使得面
折起,使得面![]() 面
面![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为________;当三棱锥
体积的最大值为________;当三棱锥![]() 体积最大时,其外接球的表面积为________.
体积最大时,其外接球的表面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”. 为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须相邻安排的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,
,![]() ,直线与曲线C交于A,B两点.
,直线与曲线C交于A,B两点.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P的极坐标为 ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com